首先$O(n^2)$的$dp$很显然

$$f[i] = min(f[i],f[j] + maxa(j+1,i))$$

其中$1 \leq i \leq n,0 \leq j < i$

观察方程,在$i$确定的时候,决策点$j$递增时,$maxa(j+1,i)$这个函数是单调不上升的,那么很容易想到利用单调队列来维护决策点(此处的单调队列维护的是$a_i$严格递减的决策集合)

但我们仍不知道决策集合中的最优决策是什么,因为$f[j]$是随决策点$j$递增而单调不下降的

同样是因为这个性质,我们知道如果当$[l,r]$的$maxa$相同,那么$f[l]+maxa(l,r)$就是相对于这个$maxa$最优值(即取左边)

口胡了半天,但实际画个图一下就懂了

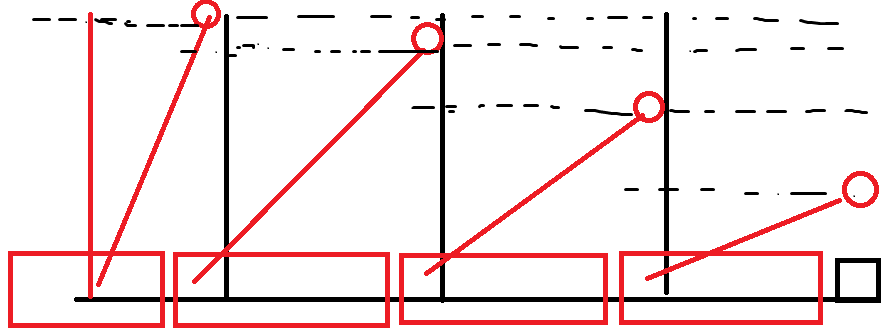
图中红点即为单调队列维护的决策点,对于每个红点,它会相应地”管控”一段区间(即那段区间的$maxa$相同,都是它)

前面我们又说了,对于$[l,r]$的$maxa$相同,我们会选最左边的$l$($f[i]$单调不下降)

又观察这个$l$与上一个决策点刚好在同一位置,那么对于每个决策点,它的权值就可以表示为$calc[x] = f[q[x]] + a[q[x+1]]$

其中$x$为决策点在队列中的编号

然后这个东西就可以用一个支持动态插入,删除,查找的数据结构维护决策集合中的权值最大值(我用的$muitlset$)

但还需注意,最左端的红点是要与此时窗口最左端的位置配对的,这个最后取最优值的时候弄一下就行了

时间复杂度 $O(nlogn)$

~~

真的是写不下去了

但还是放个具体实现方法吧

维护$a[i]$严格单调递减的决策队列,并用$set$(此处是$multiset$)维护相应的值

1. 将$a[i]$插入队列(将$q[r]$出队时也要先在$set$中删除$calc(r-1)$),并将$calc(r-1)$插入$set$

2. 维护窗口最左端($Li$)(利用前缀和维护)

3. 将非法队首出队,并在$set$中找到并删除$calc(l)$

4. $f[i] = min(f[Li-1]+a[q[l]],*s.begin())$

放代码吧

• 注 : 那个$lst$是个人单调队列习惯写法,表示的是还未加入决策集合的最左端的位置,不喜的可以看第二篇(专门改了原来的代码,不投币,点赞,收藏,三连一下吗qwq)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <set>
typedef long long ll;
using namespace std;

template <typename T>void in(T &x) {
    x = 0; T f = 1; char ch = getchar();
    while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
    while(isdigit(ch)) {x = 10*x + ch - '0'; ch = getchar();}
    x *= f;
}

template <typename T>void out(T x) {
    if(x < 0) putchar('-'),x = -x;
    if(x > 9) out(x/10);
    putchar(x%10+'0');
}

//---------------------------------------------------------------

const int N = 1e5+7;
const ll inf = 1e15;

int n,a[N];
ll m,sum[N],f[N];

int q[N],l = 1,r,lst = 0,Li = 0;

multiset <ll> s;

ll dis(int i,int j) {
    return sum[j]-sum[i-1];
}

ll calc(int x) {
    return f[q[x]]+a[q[x+1]];
}

int main() {
//  freopen("0.in","r",stdin);
    in(n); in(m);
    for(int i = 1;i <= n; ++i) {
        in(a[i]); sum[i] = sum[i-1]+a[i];
    }
//  memset(f,0x7f,sizeof(f));
    f[0] = 0; lst = 1; Li = 0;
    for(int i = 1;i <= n; ++i) {

        while(dis(lst,i) > m) ++lst;

        for(;dis(lst,i) <= m && lst <= i; ++lst) {
            while(l <= r && a[q[r]] <= a[lst]) {
                if(l < r) s.erase(s.find(calc(r-1))); 
                --r;
            }
            q[++r] = lst;
            if(l < r) s.insert(calc(r-1));
        }

        while(dis(Li,i) > m) ++Li;

        while(l <= r && q[l] < Li) {
            if(l < r) s.erase(s.find(calc(l)));
            ++l;
        }
        if(l <= r) f[i] = f[Li-1]+a[q[l]];//notice : Li-1 not Li
        if(l < r) f[i] = min(f[i],*s.begin());
    }
    out(f[n]);
    return 0;
}

你们要的写法

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <set>
#define ll long long
using namespace std; 

template <typename T> void in(T &x) {
    x = 0; T f = 1; char ch = getchar();
    while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
    while( isdigit(ch)) {x = 10 * x + ch - 48; ch = getchar();}
    x *= f;
}

template <typename T> void out(T x) {
    if(x < 0) x = -x , putchar('-');
    if(x > 9) out(x/10);
    putchar(x%10 + 48);
}
//-------------------------------------------------------

const int N = 1e5+7;

ll n,a[N],L;
ll q[N],l,r,Li,sum;
ll f[N];
multiset <ll> s;

ll calc(int x) {
    return f[q[x]]+a[q[x+1]];
}

int main() {
//    freopen("0.in","r",stdin);
    in(n); in(L);
    for(int i = 1;i <= n; ++i) in(a[i]);
//    memset(f,0x7f,sizeof(f));
    f[0] = 0; Li = 0;
    for(int i = 1;i <= n; ++i) {
        //插入
        while(l <= r && a[i] >= a[q[r]]) {
            if(l < r) s.erase(s.find(calc(r-1))); 
            --r;
        }
        q[++r] = i;
        if(l < r) s.insert(calc(r-1));

        //维护窗口最左端
        sum += a[i];
        while(sum > L) sum -= a[Li++];

        while(l <= r && q[l] < Li) {
            if(l < r) s.erase(s.find(calc(l)));
            ++l;
        }

        if(l <= r) f[i] = f[Li-1]+a[q[l]];
        if(l < r) f[i] = min(f[i],*s.begin());
    }
    out(f[n]);
    return 0;
}