题目描述

我们在一个 n*n 的网格上构建了新的迷宫地图，蛇的长度为 2，也就是说它会占去两个单元格。蛇会从左上角 (0, 0) 和 (0, 1) 开始移动。我们用 0 表示空单元格，用 1 表示障碍物。蛇需要移动到迷宫的右下角 (n-1, n-2) 和 (n-1, n-1)。

每次移动，蛇可以这样走：

• 如果没有障碍，则向右移动一个单元格。并仍然保持身体的水平／竖直状态。
• 如果没有障碍，则向下移动一个单元格。并仍然保持身体的水平／竖直状态。
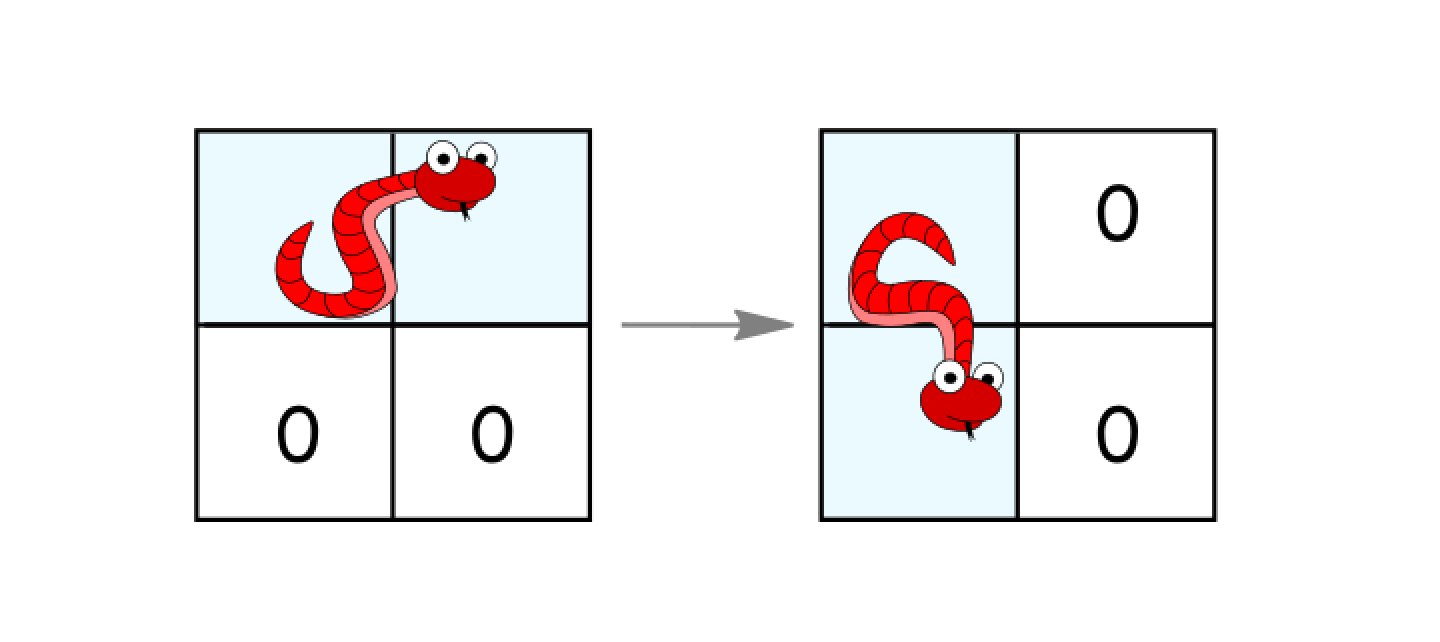
• 如果它处于水平状态并且其下面的两个单元都是空的，就顺时针旋转 90 度。蛇从 (r, c)、(r, c+1) 移动到 (r, c)、(r+1, c)。
  
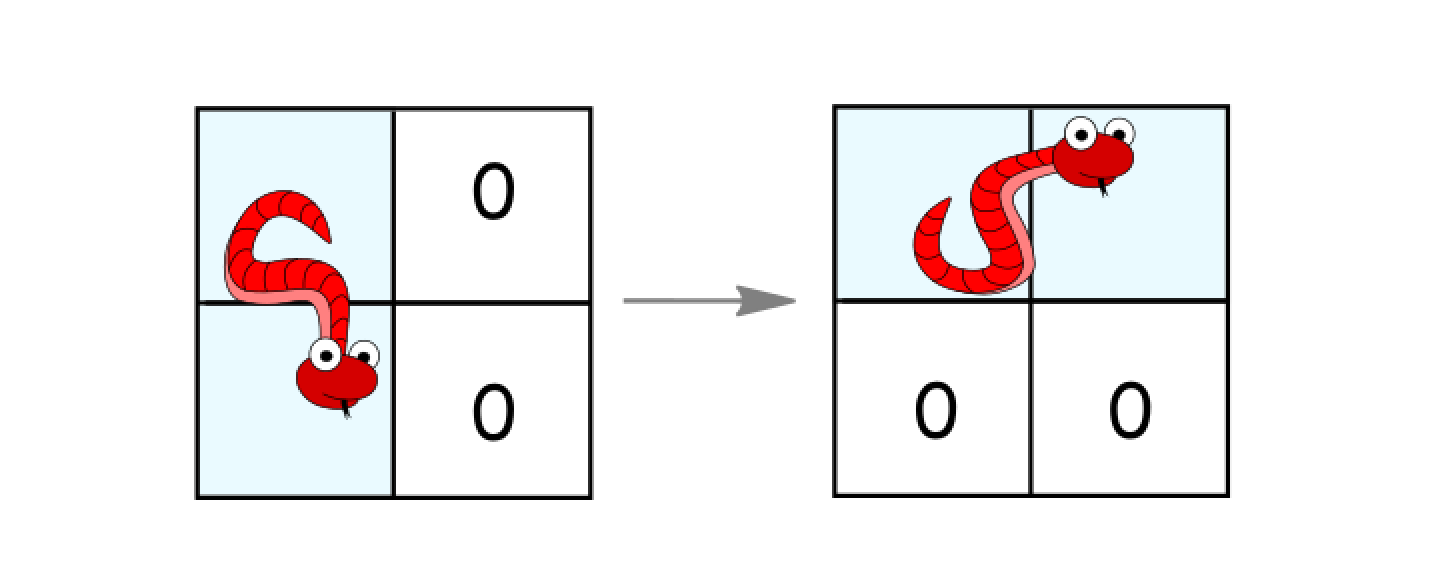
• 如果它处于竖直状态并且其右面的两个单元都是空的，就逆时针旋转 90 度。蛇从 (r, c)、(r+1, c) 移动到 (r, c)、(r, c+1)。
  

返回蛇抵达目的地所需的最少移动次数。

如果无法到达目的地，请返回 -1。

样例

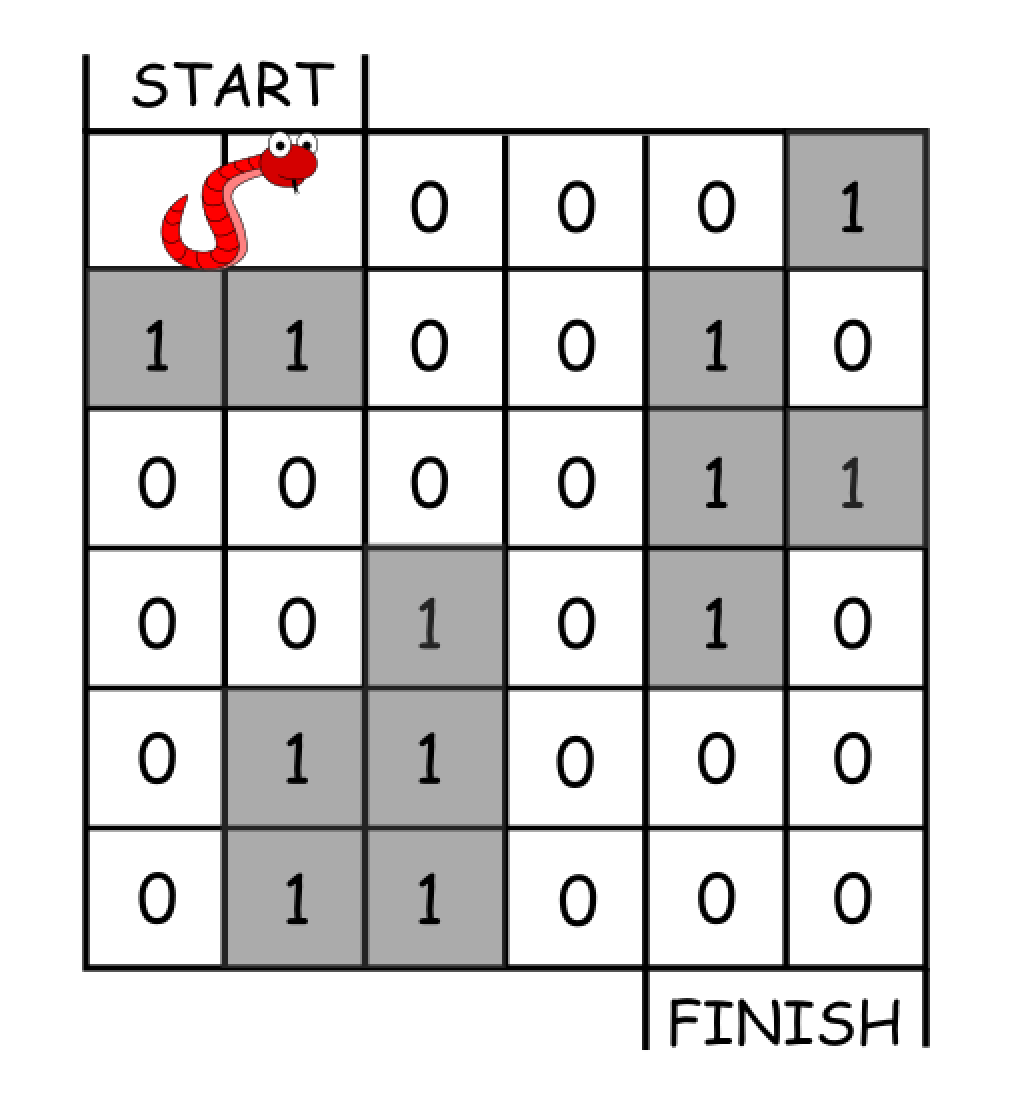
输入：grid = [[0,0,0,0,0,1],
             [1,1,0,0,1,0],
             [0,0,0,0,1,1],
             [0,0,1,0,1,0],
             [0,1,1,0,0,0],
             [0,1,1,0,0,0]]
输出：11
解释：
一种可能的解决方案是 [右, 右, 顺时针旋转, 右, 下, 下, 下, 下, 逆时针旋转, 右, 下]。

输入：grid = [[0,0,1,1,1,1],
             [0,0,0,0,1,1],
             [1,1,0,0,0,1],
             [1,1,1,0,0,1],
             [1,1,1,0,0,1],
             [1,1,1,0,0,0]]
输出：9

限制

• 2 <= n <= 100
• 0 <= grid[i][j] <= 1
• 蛇保证从空单元格开始出发。

算法

(宽度优先搜素 / BFS) $O(n^2)$

1. 宽搜的状态可以用一个三元组表示 (x, y, d)，其中 (x, y) 为蛇尾的位置，d == 0 表示蛇朝向右方，d == 1 表示蛇朝向下方。
2. 从初始位置开始宽度优先搜索，搜索过程中注意合法性和边界情况的判断。

时间复杂度

• 最多有 $O(n^2)$ 的不同状态，每个状态最多遍历一次，故时间复杂度为 $O(n^2)$。

空间复杂度

• 需要用数组记录每个状态的距离，以及用队列记录搜索过程，故空间复杂度为 $O(n^2)$。

C++ 代码

struct P {
    int x, y, d;
    P(int x_, int y_, int d_): x(x_), y(y_), d(d_) {}
};

class Solution {
public:
    int minimumMoves(vector<vector<int>>& grid) {
        int n = grid.size();

        vector<vector<vector<int>>> dis(n, vector<vector<int>>(n, vector<int>(2, -1)));

        queue<P> q;

        dis[0][0][0] = 0;
        q.push(P(0, 0, 0));

        while (!q.empty()) {
            auto sta = q.front();
            q.pop();

            if (sta.x == n - 1 && sta.y == n - 2 && sta.d == 0)
                break;

            if (sta.d == 0) { // face right
                // move right
                if (sta.y + 2 < n && grid[sta.x][sta.y + 2] == 0) {
                    if (dis[sta.x][sta.y + 1][0] == -1) {
                        dis[sta.x][sta.y + 1][0] = dis[sta.x][sta.y][0] + 1;
                        q.push(P(sta.x, sta.y + 1, 0));
                    }
                }

                // move down
                if (sta.x + 1 < n && grid[sta.x + 1][sta.y] == 0
                                  && grid[sta.x + 1][sta.y + 1] == 0) {
                    if (dis[sta.x + 1][sta.y][0] == -1) {
                        dis[sta.x + 1][sta.y][0] = dis[sta.x][sta.y][0] + 1;
                        q.push(P(sta.x + 1, sta.y, 0));
                    }
                }

                // rotate clockwise
                if (sta.x + 1 < n && grid[sta.x + 1][sta.y + 1] == 0
                                  && grid[sta.x + 1][sta.y] == 0) {

                    if (dis[sta.x][sta.y][1] == -1) {
                        dis[sta.x][sta.y][1] = dis[sta.x][sta.y][0] + 1;
                        q.push(P(sta.x, sta.y, 1));
                    }

                }
            } else { // face down
                // move right
                if (sta.y + 1 < n && grid[sta.x][sta.y + 1] == 0
                                  && grid[sta.x + 1][sta.y + 1] == 0) {
                    if (dis[sta.x][sta.y + 1][1] == -1) {
                        dis[sta.x][sta.y + 1][1] = dis[sta.x][sta.y][1] + 1;
                        q.push(P(sta.x, sta.y + 1, 1));
                    }
                }

                // move down
                if (sta.x + 2 < n && grid[sta.x + 2][sta.y] == 0) {
                    if (dis[sta.x + 1][sta.y][1] == -1) {
                        dis[sta.x + 1][sta.y][1] = dis[sta.x][sta.y][1] + 1;
                        q.push(P(sta.x + 1, sta.y, 1));
                    }
                }

                // rotate clockwise
                if (sta.y + 1 < n && grid[sta.x + 1][sta.y + 1] == 0
                                  && grid[sta.x][sta.y + 1] == 0) {

                    if (dis[sta.x][sta.y][0] == -1) {
                        dis[sta.x][sta.y][0] = dis[sta.x][sta.y][1] + 1;
                        q.push(P(sta.x, sta.y, 0));
                    }

                }
            }
        }

        return dis[n - 1][n - 2][0];
    }
};