题目描述
给定一颗树，树中包含n个结点（编号1~n）和n-1条无向边。
请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。
重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。
输入格式
第一行包含整数n，表示树的结点数。
接下来n-1行，每行包含两个整数a和b，表示点a和点b之前存在一条边。
输出格式
输出一个整数m，表示重心的所有的子树中最大的子树的结点数目。
数据范围
1≤n≤105
样例
输入样例
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样例：
4
DFS(深度优先遍历)
主要思路：
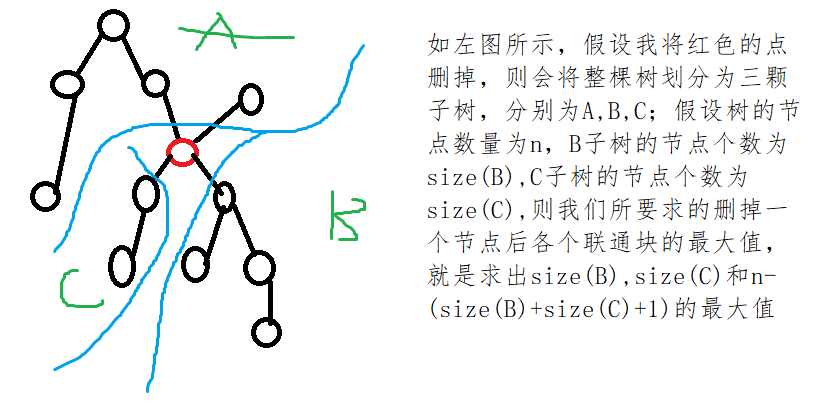
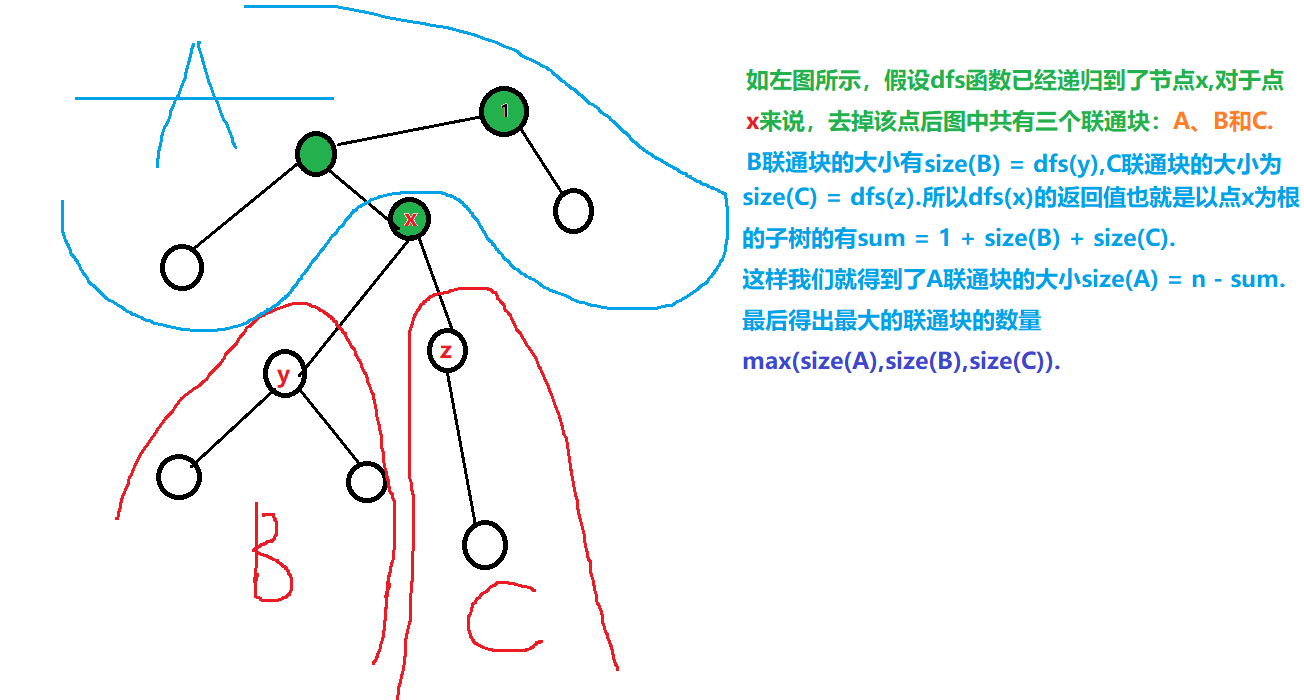
C++ 代码
#include <iostream>
#include <cstring>
using namespace std;
const int N=100010;
bool state[N];
//因为是双向边
int h[N],e[2*N],ne[2*N],idx,ans=N;
int n;
int add(int a,int b){
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
//返回的是以u为根的子树中点的数量
int dfs(int u){
//标记u这个点被搜过
state[u]=true;
//size是表示将u点去除后，剩下的子树中数量的最大值；
//sum表示以u为根的子树的点的多少，初值为1，因为已经有了u这个点
int size=0,sum=1;
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(state[j]) continue;
//s是以j为根节点的子树中点的数量
int s=dfs(j);
//
size=max(size,s);
sum+=s;
}
//n-sum表示的是减掉u为根的子树，整个树剩下的点的数量
size=max(size,n-sum);
ans=min(size,ans);
return sum;
}
int main(){
cin>>n;
memset(h,-1,sizeof h);
int a,b;
for(int i=0;i<n;i++){
cin>>a>>b;
add(a,b);
add(b,a);
}
dfs(1);
cout<<ans;
return 0;
}
注意图一右上的单支和左上的成一个连通块，那一点是个bug，应该是楼主画错了。
其他的都都挺好的，楼主真👍了，支持
图借了，thanks
这里是无向联通的~ 那怎么确定他只能访问子树，而不难向上访问父亲节点呢？？
有标记
这个图不是从4开始搜的
但是，如果从刚开始从1搜的话，1上方的节点一开始是没有被标记的啊？
这里理解不了，，求大神指导
他是无向图，从随意那个个点都可以访问到别的点
棒了
各数组啥意思呀，初学图部分者表示看不懂
佬们，想问一下，最后一次递归是什么情况啊，实在是没弄懂递归结束的条件
为什么dfs(j)是以j为根节点的子树中点的数量,代码中怎么体现出来的
OK懂了
牛逼
真的好，配合图去看，就能明白sum，size和ans是干什么的了。
大佬，dfs的值的怎么给的？为什么就给1了
不好意思dfs(）可以选任意数字
dfs(0)，答案是错的，知道为什么吗？其他的可以过掉
因为下标是从1开始的吧
编号是从1-n的，题目中说了。这里的编号也就是邻接表中的头节点，这里将所有都初始化为-1了，所以后面没有节点，遍历不了
int s=dfs(j);
//
size=max(size,s);
sum+=s;
}
//n-sum表示的是减掉u为根的子树，整个树剩下的点的数量
size=max(size,n-sum);
ans=min(size,ans);
return sum;
}
这里我没弄明白，有没有大佬讲述一下这是什么意思
为什么可以这样比较大小啊，我不太明白比较大小这里
因为要求最大的连通块，上面求的是这个点之后的最大连通块的数量，下面的是减去这个点之后的连通块最大数量，然后又因为最大值最小
为什么要返回sum啊
递归返回时，告诉父节点当前子树的连通大小
牛逼，其他没看懂，在这看懂了
这图好啊，搞懂了
其他都没看懂 唯独这个题解看懂了
为啥图一哪个右上的单支也要和左上的成一个连通块呢？
我也想问┭┮﹏┭┮
这个地方是个bug， 楼主应该是画错了，画的这就不一棵树了，成图了！！
赞👍
大赞
看了这么多，你是讲的最清楚的，点赞！
通俗易懂，赞一个
赞👍