题目描述

现在有一堆数字共N个数字（N<=$10^6$），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1 3 -1 -3 5 3 6 7], and k = 3.

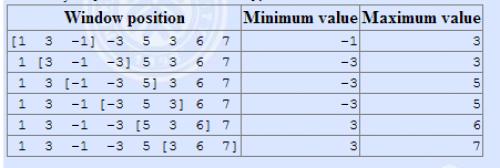
输入格式

输入一共有两行，第一行为n,k。

第二行为n个数(<INT_MAX).

输出格式

输出共两行，第一行为每次窗口滑动的最小值

第二行为每次窗口滑动的最大值

输入输出样例

输入 #1

8 3
1 3 -1 -3 5 3 6 7

输出 #1

-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明/提示

50%的数据，$n<=10^5$

100%的数据，$n<=10^6$

题解

• 单调队列模板题

• 单调队列顾名思义它是单调的（雾 因此一个队列要想是单调队列就必须要满足单调性（废话

• 那么对于本题来说我们该如何维护它的单调性呢？
• 以最小值为例
• 首先假设原数组有两个相邻元素$x, y$，如果$x>y$且$a[x]>a[y]$ ，那么$x$无疑没有$y$优秀。以为$x$的值更大且更靠前，那么在窗口的滑动过程中，$x$一定先比$y$出队
• 根据上面的性质我们就可以推出单调队列的更新方式。 即当循环到$i$时，判断队尾与$a[i]$的大小关系。如果$a[tail]>=a[i]$则将$tail$出队，知道不能再更新为止。 然后判断对头在原数组中的位置与$i$是否相差$k$，将对头出队。当队列合法时，对头即为所求答案
• 最大值同理

code

#include <bits/stdc++.h> 
using namespace std; 
const int maxn = 1e6 + 100; 

template <class T> 
inline void read(T &s) {
    s = 0; T w = 1, ch = getchar(); 
    while (!isdigit(ch)) { if (ch == '-') w = -1; ch = getchar(); }
    while (isdigit(ch)) { s = (s << 1) + (s << 3) + (ch ^ 48); ch = getchar(); }
    s *= w; 
}

int n, k; 
int a[maxn], q[maxn], p[maxn]; 

void get_max() {
    int head = 1, tail = 0; 
    for (int i = 1; i <= n; ++i) {
        while (head <= tail && q[tail] <= a[i]) tail--; 
        q[++tail] = a[i]; p[tail] = i; 
        while (p[head] <= i - k) ++head; 
        if (i >= k) printf("%d ", q[head]); 
    }
}

void get_min() {
    int head = 1, tail = 0; 
    for (int i = 1; i <= n; ++i) {
        while (head <= tail && q[tail] >= a[i]) tail--; 
        q[++tail] = a[i]; p[tail] = i; 
        while (p[head] <= i - k) ++head; 
        if (i >= k) printf("%d ", q[head]); 
    }
    puts(""); 
}

int main() {
    read(n), read(k); 
    for (int i = 1; i <= n; ++i) read(a[i]); 

    get_min(); 
    get_max(); 
    return 0; 
}