前缀表达式和后缀表达式

计算常见的数学公式 1 * 2 + 3 * 4

后缀表达式 [1 2 * 3 4 * +] ：从左往右遍历时 这里每次在遇到运算符以前一定先经过了2个数字
中缀表达式 [1 * 2 + 3 * 4] :从左往右遍历时 这里每次再遇到运算符以前还不知道另外一个数字是什么

我们能够发现，平时我们书写公式时用的便是中缀的形式，即在运算符的两侧添加两个数字完成一次运算，但是对编程来说，后缀表达式是更加方便的，每次只需要在遇到运算符时，拿出来已经遍历的2个数进行一次运算即可，详细讨论如下。现在我们来建一颗 1 * 2 + 3 * 4 的树， 如下图所示:

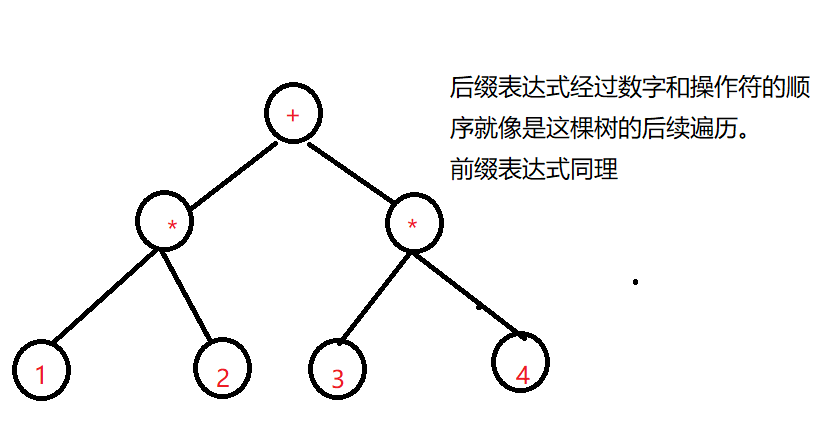
再模仿计算过程时，我们能够发现叶子节点都是需要进行运算的数字并且子树都需要先算，无论是中缀还是后缀表达式，其对应的计算公式实际是相同的，其生成的树也必须是相同的，所不同的是遍历的顺序不一样。接下来我们来建一颗 1 + 2 * 3 + 4 的计算树

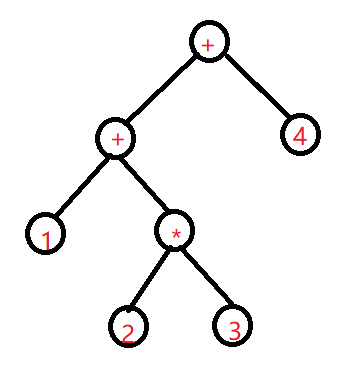
我们对他进行后序遍历，从前往后依次是 1 2 3 * + 4 +, 可以发现后序遍历的好处了，在遇到的第一个预算符号 * 时，只需要弹出数字栈中的两个数字 2 和 3， 计算 2 * 3 = 6， 将6压入到数字栈中，就变成了 1 6 + 4 + ，又可以进行运算了 1 + 6 = 7, 变成 7 4 +。 这种遍历的方式就是在树上进行后序遍历，无疑对计算机来说是实现运算最为简单的方式了。并且我们将这种计算方式模板化为 eval() 操作 , 如下

eval()

void eval()
{
    auto b = num.top(); num.pop();
    auto a = num.top(); num.pop();
    auto c = op.top(); op.pop();
    int x;
    if (c == '+') x = a + b;
    else if (c == '-') x = a - b;
    else if (c == '*') x = a * b;
    else x = a / b;
    num.push(x);
}

我们平时自己写的公式形式如何让计算机能够运算？

但是又回到了原本的话题上了，这棵树是我们建的，不是随便给一个中缀表达式计算机就能够生成的，每一个数学公式(前缀表达式和中缀表达式代表相同的一个数学公式）可以这样映射到1棵树上，但是我们书写的是中缀表达式的形式，中缀表达式是不能直接像后缀表达式一样从左往右的依次计算的，因为中序遍历时，每一个运算符的右儿子们是还没有被遍历的。
难道每次计算的时候，我们要根据数学表达式建立一颗树，在对这颗树进行后序遍历吗？

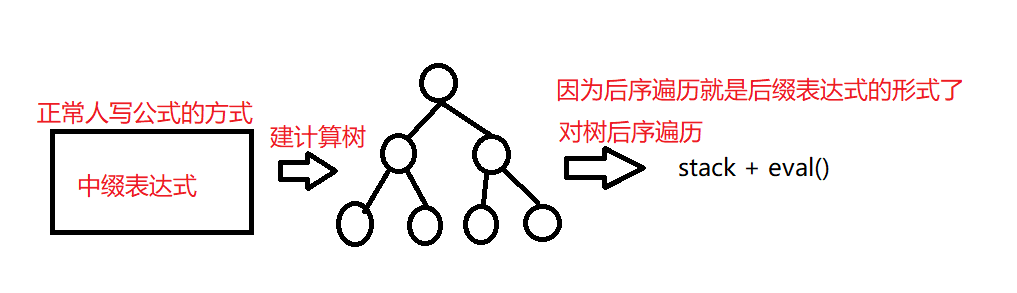
可以这样做。 但也可以发挥能动性找规律。问题就变成了 在中缀表达式 1 + 2 * 3 + 4 中，我们什么时候能进行运算？

解： 我们第一次遇到的运算符是 + 号，此时计算明显是不合理的，一来右子树还不知道是什么，二来下一个操作符也不知道是什么。接着往右遍历，遇到第2个运算符了，虽然 * 号有着更高的优先级，但我们还是不知道 * 号的右边的数字是什么。接着往右遍历，这次是 + 号了，magic的逻辑来了，虽然 + 号的右侧数字我还是不知道是啥，但是 + 号不是第一个遇到的运算符，+ 号左边至少有1个操作符，两个数字，且左边最近的运算符是 * 号，他的优先级是高于 + 号的，也就是说 * 号应该比此时的 + 号先算，并且 * 号两边要参加计算的数我们是知道的，我们计算完 2 * 3 以后，一下子问题就变成了 1 + 6 + 4 了。注意此时我们还是停留在第2个 + 号上，还没有继续往后遍历，这个时候 第2个 + 号的前面还有 1个 + 号，并且前面那个+号要加的数我都知道了，1 + 6 计算之后，问题一下子又能前进一步了 变成 7 + 4 , 这时候只有1个数字，1个运算符了，是不能进行计算的。我们没办法，继续往后遍历，遍历完了都没有再遇到运算符了，但这个时候 我知道 + 号的一边是 7，一边是4，问题解决，答案就是 7 + 4 = 11。

括号的作用 – 括号里面相当于子公式 对于树来说等价于计算好的值

问题还没完，就是我们书写公式的形式，他是有括号的，虽然括号不是运算符，也不是数字，但他影响到了整个计算的次序，另外一方面，1+2 * (3 + 4) 和 1+2 * 3+4 显然不是同一个公式，自然也不能抽象成同一棵树，所以对于 1 + 2 * (3 + 4) , 先把他抽象成树

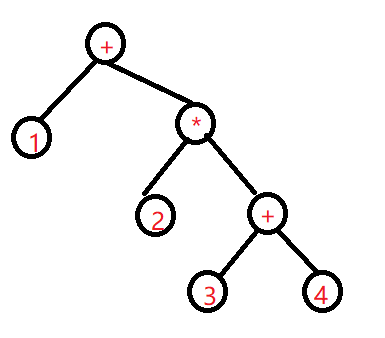
这棵树明显和前面的两棵树都不一样了，因为公式本身就不一样。这时候又需要找规律了，首先为什么要加“()”号，是因为低优先级的运算需要先进行运算 ， 而在我们遇到 ‘)’ 时，”(” 和 “)” 内的部分一定已经遍历过了，朴素的来看，无论(dadafafasdsafaf)内是怎么样， ()里面的内容实际上就是一个子公式
对子公式的运算实际上也应该和原公式一样，上一节我们遍历到最后是 7 + 4 , 那么子公式里，遍历到最后抽象成最简单的形式也无非是 (a + b) , (a * b)，做一次运算即可。

计算过程图示

作者：Hasity
链接：https://www.acwing.com/solution/content/40978/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

为什么如果栈顶的运算符优先级大于即将要入栈的运算符 就要进行运算

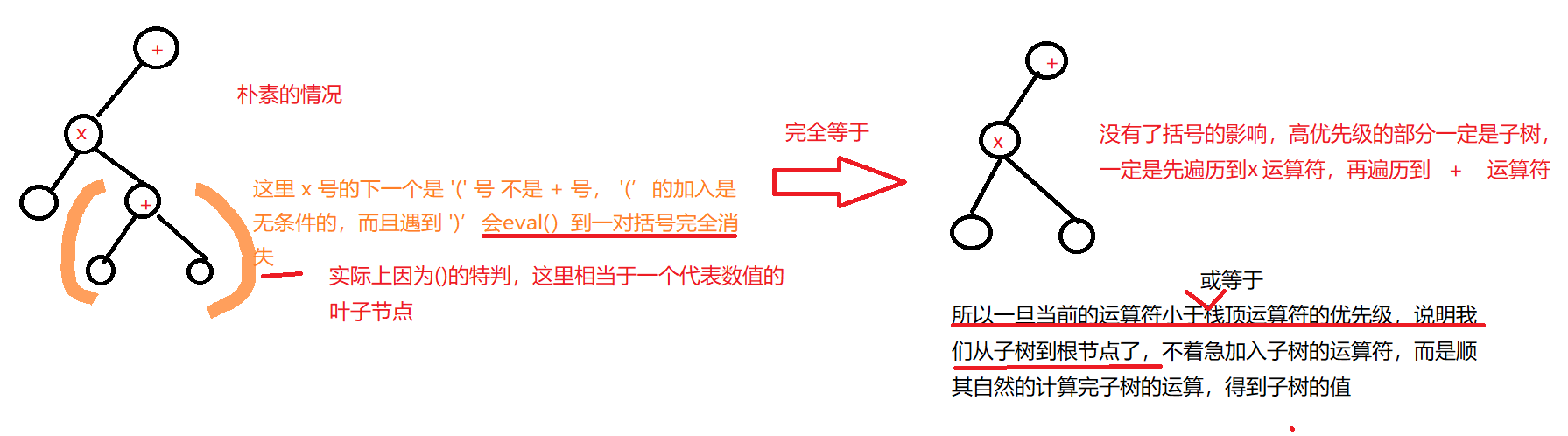
如图，在中缀表达式中难免会有括号，但括号会影响到优先级的，按照常理来说，加号的优先级低于乘号，但是由于括号的作用，构建的计算树出现了低优先级变成子树先计算的情况，但是不要担心，因为括号的特判，每次匹配到一对括号的时候，会计算完括号里所有的运算并等于1个数，也就是说有括号的情况最后会等于没括号的情况，如同图片的左边，为什么栈顶的运算符优先级大于即将要入栈的运算符，就要进行运算，就是因为一旦出现当前运算符的优先级小于栈顶元素优先级的时候，就意味着栈顶运算符所代表的整个子树已经遍历完了，现在是在从子树返回根节点的时候，所以理所当然的应当要计算完整个子树，再把当前运算符加入到栈中了.

code

#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
#include <unordered_map>

using namespace std;

stack<int> num;
stack<char> op;

void eval() // 弹出两个数和一个运算符，在树里面就是弹出一个3个节点的子树, 经过处理以后在压回去一个叶子节点
{
    int b = num.top(); num.pop();
    int a = num.top(); num.pop();
    char c = op.top(); op.pop();

    int x = 0;

    if (c == '+') x = a + b;
    else if (c == '-') x = a - b;
    else if (c == '*') x = a * b;
    else x = a / b;

    num.push(x);
}

bool is_digit(char c)
{
    if (c >= '0' && c <= '9') return true;
    else return false;
}

int main()
{
    string s;
    cin >> s;

    unordered_map<char, int> pr{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};

    for (int i = 0; i < s.size(); i ++ )
    {
        char c = s[i];

        if (is_digit(c)) // 如果是数字
        {
            int x = 0, j = i;
            while (j < s.size() && is_digit(s[j])) x = x * 10 + s[j ++ ] - '0';
            i = j - 1; // 巧妙的让 i ++ 从下一个不是数字的字符位置开始 
            num.push(x);
        }
        else if (c == '(') op.push(c);  
        else if (c == ')') 
        {
            while (op.top() != '(') eval();  // op里一定有一个 '(' 所以一定不为空, () 内的部分要全部运算完成1个数
            op.pop(); // 弹出 '('
        }
        else
        {
            // 如果当前子树已经遍历完了，遍历到了根节点上(根节点是一个优先级小于子树的根节点运算符的运算符)
            while (op.size() && op.top() != '(' && pr[op.top()] >= pr[c]) eval(); // 如果栈顶的运算符大于等于当前的运算符 

            op.push(c);
        }
    }

    while (op.size()) eval();

    cout << num.top() << endl;
}