算法：数学 + 二分

这题是个思维题，想到了很简单，没想到得做很久，当时我直接二维模拟做，估计能骗30分

首先我们都知道，杨辉三角就是组合数，每一个数都可以被表示出来

如图所示，杨辉三角是左右对称的，所以我们只用看一半即可

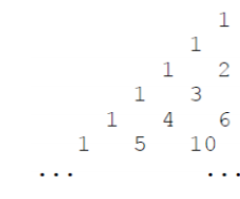
这里我们斜着看每一行，也就是这样看

我们可以从图中发现除了第一行外，每一行都是单调递增的，又因为杨辉三角就是组合数，所以每一行的最小值可以表示为 $C_{2k}^{k}$ $k$ 是当前行（横着）第几个数如图所示

因为是斜着的每一行是单调递增的，所以我们可以用二分来找到目标值 $n$， 又因为每一斜行也是单调递增的，所以我们从最里面开始往外找

• 上边界 $l = 2k$
• 下边界 $r = n$ （如果内层斜行都没找到，一定出现在第2行，因为$C_{n}^{1} = n$）

我们知道组合数越靠近中间越大，所以由 $n$ 的范围是 $10^9$ 可以通过计算器算出 $C_{34}^{17} > 10^9, C_{32}^{16} < 10^9$

所以我们可以枚举每一斜行的开头元素（最小元素）$k$, 从 $16$ 开始枚举

二分的check就是 如果 $C_{mid}^{k} >= n$，取左区间，否则取右区间

当我们找到了这个数的时候即 $C_{r}^{k} == n$

我们通过找规律发现 $r$ 为前面共多少行（不算这一行），第一行有 $1$ 个数，第二行有 $2$ 个数，第三行有 $3$ 个数，第 $n$ 行有 $n$ 个数，也就是前面一共有 $\frac{r(1 +r)}{2}$ 个数， $k$ 为这一行第几个（下标都从 $0$ 开始）,所以这个数是第 $\frac{r(1 +r)}{2} + k + 1$ 个数

注意： 特判第一个数 $1$

代码：

import java.util.Scanner;

public class Main {

    static int n;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        if (n == 1) {
            System.out.println(1);
            return;
        }
        for (int k = 16; ; k -- ) {
            if (check(k)) break;
        }
    }

    private static boolean check(int k) {
        long l = k * 2, r = n;
        while (l < r) {
            long mid = l + r >> 1;
            if (C(mid, k) >= n) r = mid;
            else l = mid + 1;
        }

        if (C(r, k) != n) return false;

        System.out.println(r * (r + 1) / 2 + k + 1);

        return true;
    }

    //求组合数
    private static long C(long a, long b) {
        long res = 1;
        for (long i = a, j = 1; j <= b; i --, j ++ ) {
            res = res * i / j;
            if (res > n) return res;
        }
        return res;
    }

}