未完，先鸽一段时间

邻接表

那么什么是邻接表呢？

图的邻接表存储方法跟树的孩子链表示法相类似，是一种顺序分配和链式分配相结合的存储结构。（相当于没说是吧hhh）

在图论中，我们常用V(vertex)来表示顶点，E(edge)来表示边。

先看一个图，图右就是一个邻接表的表示方法

根据vector可变长的特点，我们可以用一个vector数组h[N]来储存V。(当然不用也可以)
h[i]储存 $V_i$ 可到达的顶点

然后我们再来回忆一遍题意：

给你一颗有根树，输出从根节点root到叶节点的最长的长度，并输出路径。如果路径有多条，输出序列更小的路径。

可能有人会对题意有点懵啊，看下图。我再做解释。注：左下方这里是（0，n-1）

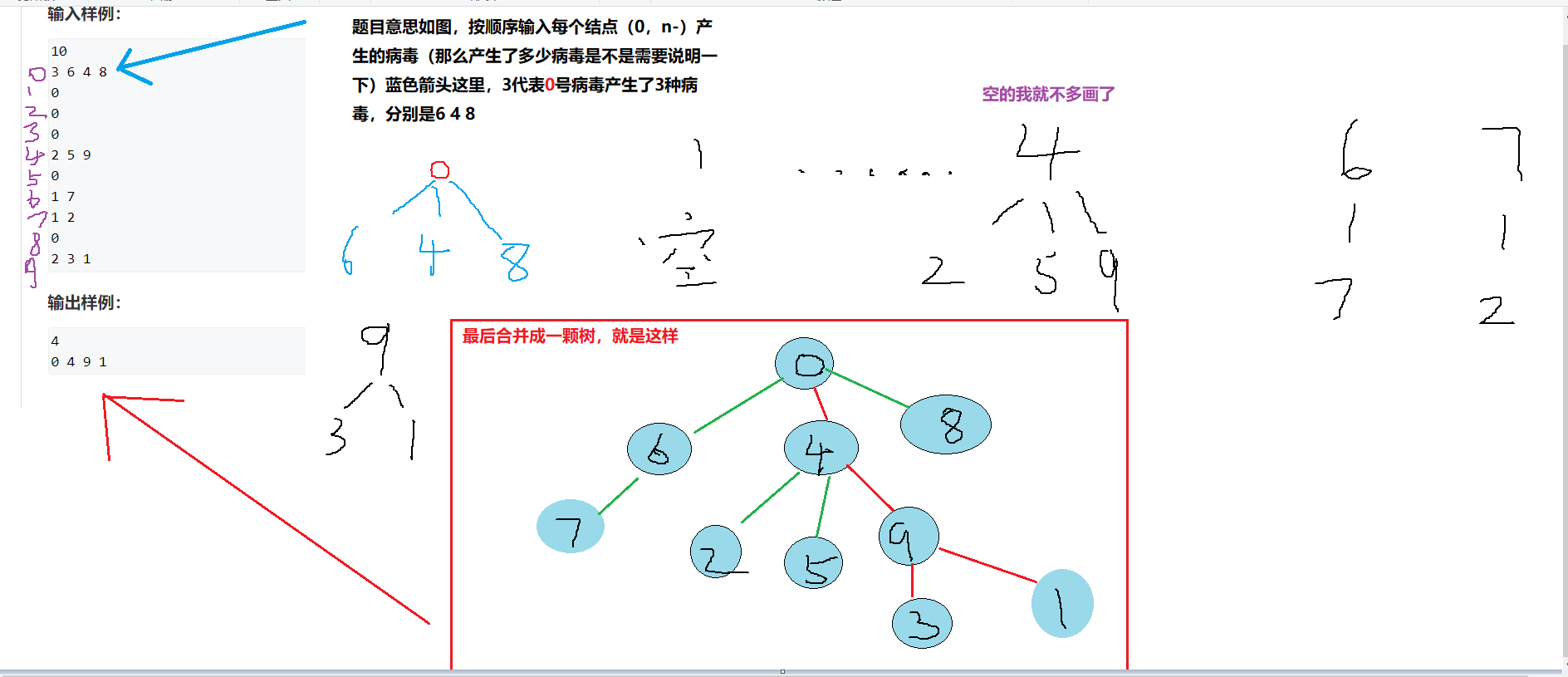
想必到这里，题目意思大家应该都能理解了吧（如果我讲的不够清楚，烦请指正，谢谢！！！）

思路部分

1. 那么第一步，我们当然是要建树啦。前面我们说的邻接表此时就派上了用场了啦

 for (int i = 0; i < n; i ++ )//依次对每个结点读入子树，并将所有树合并成一棵树
    {
        int cnt;//子节点的个数
        scanf("%d", &cnt);
        while (cnt -- )
        {
            int x;
            scanf("%d", &x);
            add(i, x);//将结点与他的父节点联系起来，这里就是邻接表的用处啦，我们在add函数中再做解释
            vis[x] = true;//为什么要有这个呢？发现没，我们树是建好了，根节点是谁啊？不知道嘛是不是。
            //但是根节点的概念是啥呢，大声说出来——没有父结点的结点对吧，所以我们需要将每一个有父节点的结点
            //表示为true，说明他有父节点，那么一会儿我们遍历一下每一个结点，不就知道谁没有父节点了吗。
            //这样我们就找到了根节点root
        }
    }

//add 函数的实现 一开始 idx=0
void add(int a, int b)  // 添加一条a->b (a到b的边)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
    /*add函数：邻接表加边
      e[i]存的是当前结点
      ne[i] 存的是单链表中下一个结点“序号”
      idx 就是单链表中的“序号”


    */
}

 int root = 0;
 while (st[root]) root ++ ;
// 搜索根节点，这应该很好理解了

 printf("%d\n", dfs(root));
//搜索最长路径，采用dfs

//这里是dfs的实现细节
//这里的dfs意思为搜索u结点到叶节点的最长路径值

int dfs(int u)
{
    int res = 0;
    son[u] = -1;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        int d = dfs(j);
        if (res < d) res = d, son[u] = j;
        else if (res == d) son[u] = min(son[u], j);
    }
    return res + 1;
}