分析

• 本题的考点：动态规划。

• 分析如下：

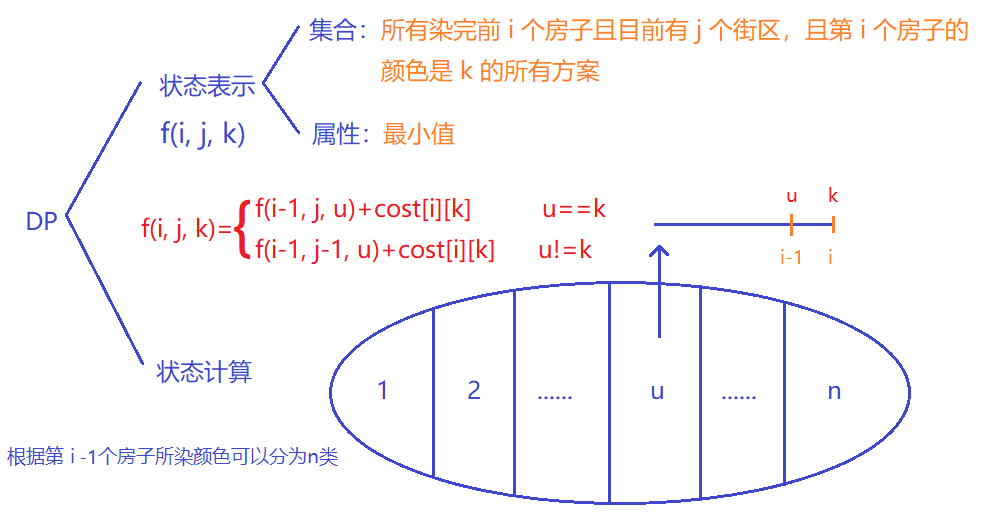
• 初始化：初始都为正无穷，然后考虑第一个房子的初始化，如果第0个房子有颜色k，则f[0][1][k]=0，否则f[0][1][i]=cost[0][i-1], i=1~n。

代码

• C++

class Solution {
public:
    int minCost(vector<int>& hs, vector<vector<int>>& cost, int m, int n, int target) {

        const int INF = 1e8;
        // 0~m-1一共m个房子，街区1~target个，颜色1~n
        vector<vector<vector<int>>> f(m, vector<vector<int>>(target + 1, vector<int>(n + 1, INF)));
        // 初始化
        if (hs[0]) f[0][1][hs[0]] = 0;
        else {
            for (int i = 1; i <= n; i++) f[0][1][i] = cost[0][i - 1];  // 将第0个房子染成i的代价
        }

        for (int i = 1; i < m; i++)  // 循环第一维：房子
            for (int j = 1; j <= target; j++) {  // 循环第二维：街区数量
                if (hs[i]) {  // 说明第i个房子已经有颜色
                    int k = hs[i];
                    for (int u = 1; u <= n; u++) {  // 循环第三维：第i-1个房子的颜色
                        if (u == k) f[i][j][k] = min(f[i][j][k], f[i - 1][j][u]);
                        else f[i][j][k] = min(f[i][j][k], f[i - 1][j - 1][u]);
                    }
                } else {
                    for (int k = 1; k <= n; k++)  // 循环第三维：第i个房子的颜色
                        for (int u = 1; u <= n; u++) {  // 循环第三维：第i-1个房子的颜色
                            if (u == k) f[i][j][k] = min(f[i][j][k], f[i - 1][j][u] + cost[i][k - 1]);
                            else f[i][j][k] = min(f[i][j][k], f[i - 1][j - 1][u] + cost[i][k - 1]);
                        }
                }
            }
        int res = INF;
        for (int i = 1; i <= n; i++) res = min(res, f[m - 1][target][i]);
        if (res == INF) res = -1;
        return res;
    }
};

• Java

class Solution {

    static final int INF = (int) 1e8;

    public int minCost(int[] hs, int[][] cost, int m, int n, int target) {
        // 0~m-1一共m个房子，街区1~target个，颜色1~n
        int[][][] f = new int[m][target + 1][n + 1];
        for (int i = 0; i < m; i++)
            for (int j = 0; j <= target; j++)
                Arrays.fill(f[i][j], INF);
        // 初始化
        if (hs[0] != 0) f[0][1][hs[0]] = 0;
        else {
            for (int i = 1; i <= n; i++) f[0][1][i] = cost[0][i - 1];  // 将第0个房子染成i的代价
        }

        for (int i = 1; i < m; i++)  // 循环第一维：房子
            for (int j = 1; j <= target; j++) {  // 循环第二维：街区数量
                if (hs[i] != 0) {  // 说明第i个房子已经有颜色
                    int k = hs[i];
                    for (int u = 1; u <= n; u++) {  // 循环第三维：第i-1个房子的颜色
                        if (u == k) f[i][j][k] = Math.min(f[i][j][k], f[i - 1][j][u]);
                        else f[i][j][k] = Math.min(f[i][j][k], f[i - 1][j - 1][u]);
                    }
                } else {
                    for (int k = 1; k <= n; k++)  // 循环第三维：第i个房子的颜色
                        for (int u = 1; u <= n; u++) {  // 循环第三维：第i-1个房子的颜色
                            if (u == k) f[i][j][k] = Math.min(f[i][j][k], f[i - 1][j][u] + cost[i][k - 1]);
                            else f[i][j][k] = Math.min(f[i][j][k], f[i - 1][j - 1][u] + cost[i][k - 1]);
                        }
                }
            }
        int res = INF;
        for (int i = 1; i <= n; i++) res = Math.min(res, f[m - 1][target][i]);
        if (res == INF) res = -1;
        return res;
    }
}

时空复杂度分析

• 时间复杂度：$O(m \times target \times n^2)$，m为房屋数量，target为需要的街区数量，n为颜色数量。

• 空间复杂度：$O(m \times target \times n)$。