题目描述

现有一盒含N块巧克力的巧克力盒（1≤N≤20），每天可以吃一块或者两块巧克力。
若每天都吃巧克力，问共有多少种不同的吃完巧克力的方案。
例如：如果 N=1，则名名第 1 天就吃掉它，共有 1 种方案；如果 N=2，则名名可以第 1 天吃 1 块，第 2 天吃 1 块，也可以第 1 天吃 2 块，共有 2 种方案；如果 N=3，则名名第 1 天可以吃 1 块，剩 2 块，也可以第 1 天吃 2 块剩 1 块，所以名名共有 2+1=3 种方案；如果 N=4，则名名可以第 1 天吃 1 块，剩 3 块，也可以第 1 天吃 2 块，剩 2 块，共有 3+2=5 种方案。

输入样例

5

输出样例

8

排列组合算法

从特殊情况分析，假设有五块巧克力：
（1）保证每天吃1块，共吃五天。共1种方案。
（2）我们将（1）中最后一天的巧克力取走，分配到前四天中。由排列组合知识可知共C(4,1)=4种方案。
（3）我们将（1）中最后两天的巧克力取走，分配到前三天中。同理可知共C(3,2)=3种方案。
（4）求和，共8种方案。
*为了便于后续推导可以将（1）的描述改为：
（5）我们将（1）中最后零天的巧克力取走，分配到前五天中。可知共C(5,0)=1种方案。
附图如下：

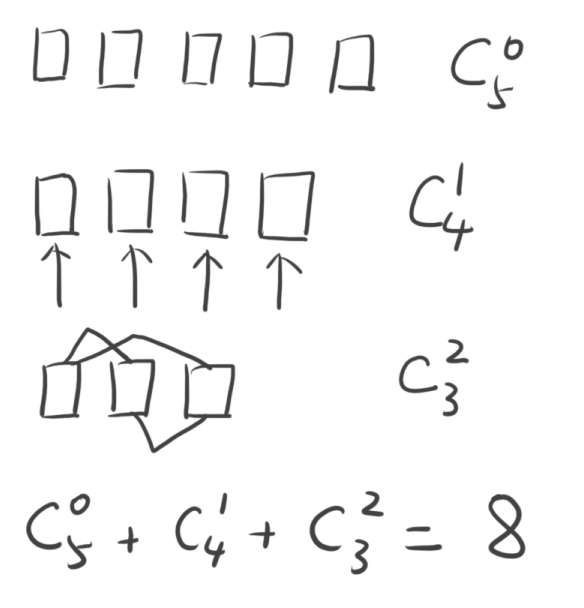
根据上述分析，我们试着推导出通项公式：
由N=5的特殊情况可以发现，答案A5=C(5,0)+C(4,1)+C(3,2)=8
推广到一般情况，可以写成一个组合数的求和式。
对于N为奇数时的边界情况，可以发现：
1.边界情况时m+1=n
2.组合数中的m（即上式中的0,1,2）的边界为N/2向下取整
3.组合数中的n（即上式中的5,4,3）的边界为N/2向上取整
上述描述的2和3在N为偶数时也成立（边界情况时m=n）
推导附图如下：

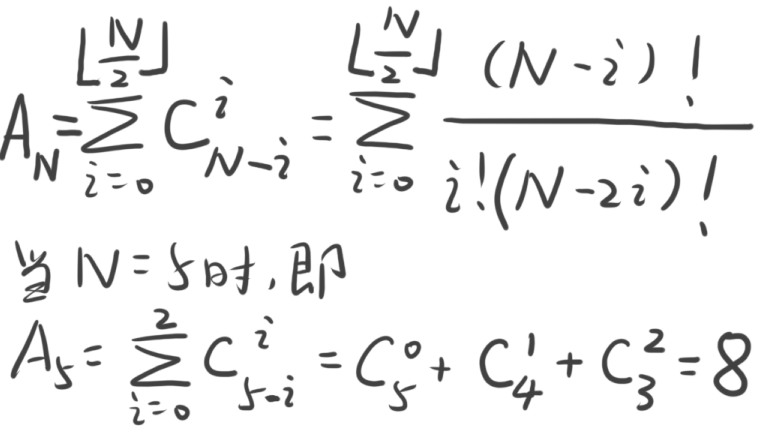
C++ 代码

#include <iostream>
using namespace std;
typedef long double ld;
ld Fac(int n) {
    if (n == 0 or n == 1) return 1.0L;
    else return n * Fac(n - 1);
}
int Comb(int n, int m) {
    return Fac(n) / (Fac(m) * Fac(n - m));
}
int main() {
    int N;
    cin >> N;
    int ans = 0;
    for (int i = 0; i <= N / 2; ++i)
        ans += Comb(N - i, i);
    cout << ans << endl;
    return 0;
}