题解一：容易理解

思路：

• 由于每个整数都是由32位二进制组成，同一个数出现三次，则第i位二进制1或0累积一定是3！
• 除了出现一次的数之外的所有数的第i位的二进制的1或0一定是3的倍数！
• 因此可以直接统计所有数的第i位1或0的情况，若不是3的倍数那一定是因为出现一次的数的原因！
• 则直接将该位累积起来即可！

参考代码：

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int res = 0, cnt = 0;
        for(int i = 0; i < 32; i ++){
            cnt = 0;
            for(auto x : nums) cnt += x >> i & 1;
            res += (cnt % 3) << i;
        }
        return res;
    }
};

题解二：不太好理解

思路：

• 依次考虑每一位数，统计每一位的累积结果
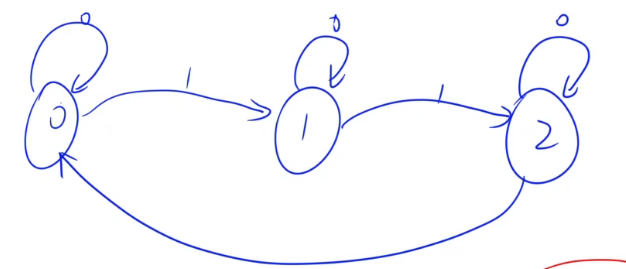
• 累积结果模3一定是0,1,2三种情况，类似状态机
• 考虑下一位最后一个二进制位为0或1的情况，可以将状态机之间的转移关系画出来！
• 对于三种状态我们可以用两个二进制为表示（0 -> 00， 1 -> 01， 2 -> 10）
• 我们用one表示最后一个二进制位，用two表示倒数第二个二进制位，如下：

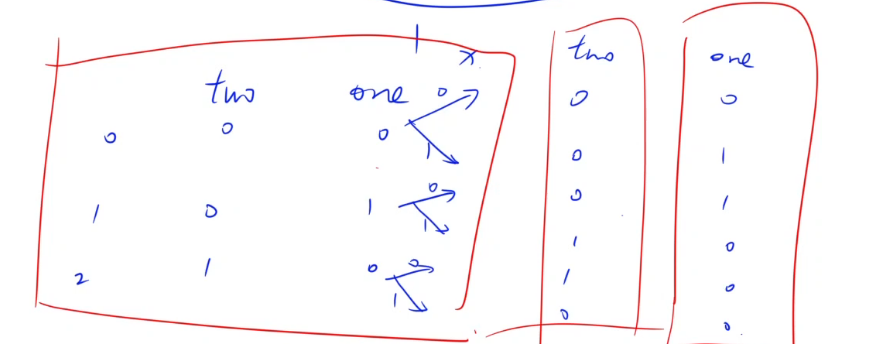
• 对于下一个数字x，最后一位二进制只能是0或1，这样我们就将这个数理逻辑图表示了出来！

关键点：如何用位运算表示出来这些情况？
结论：
one = (one ^ x) & ~two
two = (two ^ x) & ~one

• 会发现带入上面的数理逻辑图完全是正确的！

那么最终答案又是什么？

• 会发现本题中最后1的个数要么模3余0要么模3余1，因此从数理逻辑图的前两行选
• 会发现模3余0，one对应的就是0，模3余1，one对应的就是1
• 因此答案就是one

参考代码：

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int one = 0, two = 0;
        for(auto x : nums){
            one = (one ^ x) & ~two;
            two = (two ^ x) & ~one;
        }
        return one;
    }
};