题目描述

某乐团的演出场地可视作 num * num 的二维矩阵 grid（左上角坐标为 [0,0])，每个位置站有一位成员。乐团共有 9 种乐器，乐器编号为 1~9，每位成员持有 1 个乐器。

为保证声乐混合效果，成员站位规则为：自 grid 左上角开始顺时针螺旋形向内循环以 1，2，...，9 循环重复排列。例如当 num = 5 时，站位如图所示

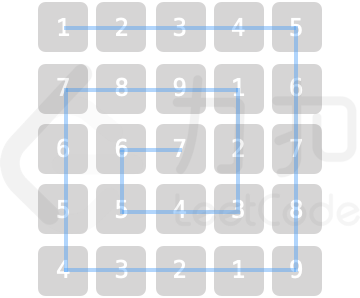
请返回位于场地坐标 [Xpos,Ypos] 的成员所持乐器编号。

样例

输入：num = 3, Xpos = 0, Ypos = 2
输出：3

输入：num = 4, Xpos = 1, Ypos = 2
输出：5

限制

• 1 <= num <= 10^9
• 0 <= Xpos, Ypos < num

算法

(找规律) $O(1)$

1. 第一步定位给定的坐标所在的层数：m = min(xPos, num - 1 - xPos, yPos, nums - 1 - yPos)。
2. 通过等差数列求和，计算在该层数之外的路径长度。
3. 令 xPos -= m，yPos -= m，将坐标平移到较小的矩形的边上。
4. 如果在矩形的上边界或者右边界上，则长度累加 xPos + yPos。
5. 否则，长度累加 (len - 1) * 4 - (xPos + yPos)，其中 len 为较小矩形的边长。

时间复杂度

• 仅需要常数的时间。

空间复杂度

• 仅需要常数的额外空间。

C++ 代码

#define LL long long

class Solution {
public:
    int orchestraLayout(int num, int xPos, int yPos) {
        LL m = min(min(xPos, num - 1 - xPos), min(yPos, num - 1 - yPos));
        LL s = num - 1;
        LL t = num - 1 - (m - 1) * 2;

        LL tot = (s + t) * m * 2 % 9;

        LL len = t - 1;
        xPos -= m;
        yPos -= m;

        if (xPos == 0 || yPos == len - 1)
            tot = (tot + xPos + yPos) % 9;
        else
            tot = (tot + (len - 1) * 4 - (xPos + yPos)) % 9;

        return tot + 1;
    }
};