问题定义

给定一个如下图所示的数字三角形，从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点，一直走到底层，要求找出一条路径，使路径上的数字的和最大。
       7
     3   8
   8   1   0
 2   7   4   4
4   5   2   6   5
输入格式
第一行包含整数 n，表示数字三角形的层数。
接下来 n 行，每行包含若干整数，其中第 i 行表示数字三角形第 i 层包含的整数。
输出格式
输出一个整数，表示最大的路径数字和。
数据范围
1≤n≤500,
−10000≤三角形中的整数≤10000
输入样例：
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出样例：
30

状态分析

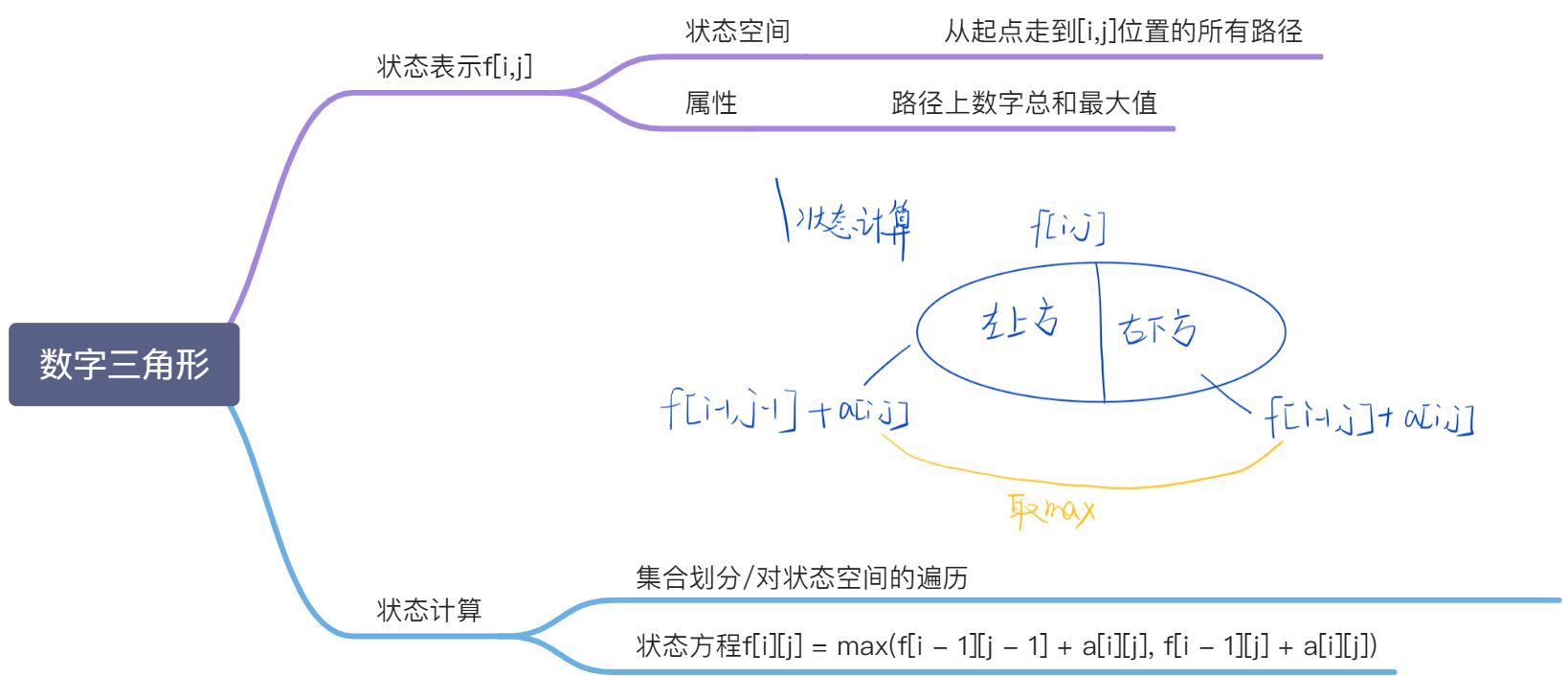
思路

• 最大值=max(左侧路径最大值+a[i][j],右侧路径最大值+a[i][j])
• 这里左侧是按例子来,存储的时候是正上方和右上方
• 初始化要把距离设为-∞
• 最后到最后一行找最大值
• 可以滚动数组优化

详细注释代码I

//@空间未优化版本
#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 510, inf = 1e9;

int f[N][N];
int a[N][N];

int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= i; ++j) {
            cin >> a[i][j];
        }
    }
    for (int i = 0; i <= n; ++i) {          //! 从0开始初始化并初始化到i+1,因为左右边界点会访问0和i+1的位置
        for (int j = 0; j <= i + 1; ++j) {  //考虑数字中有负值时,如果走了几步负值然后访问未初始化的0就会选择0
            f[i][j] = -inf;
        }
    }
    f[1][1] = a[1][1];  //第一个值
    for (int i = 2; i <= n; i++) {
        for (int j = 1; j <= i; j++) {
            f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);
        }
    }
    int res = -inf;
    for (int i = 1; i <= n; i++) {
        res = max(f[n][i], res);  //最后一行找最大值
    }
    cout << res << endl;

    return 0;
}

滚动数组优化/自底向上遍历

• 从下向上遍历,最后f[1]就是最大值
• 初始化把f初始化为最后一行的值
• 从底向上计算先考虑二维,f[i][j]的值等于下面一行f[i+1][j],f[i+1][j+1]取最大+a[i][j]
• 转移方程f[j] = a[i][j] + max(f[j], f[j + 1]); f[j]相当于下面一行的值,f[j+1]是右下方的值

详细注释代码II

//@空间优化版本 自底向上求解 滚动数组优化
#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 510, inf = 1e9;

int f[N];
int a[N][N];

int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= i; ++j) {
            cin >> a[i][j];
        }
    }
    for (int i = 1; i <= n; ++i) {
        f[i] = a[n][i];  //初始化为最下面一层的值
    }
    for (int i = n - 1; i >= 1; i--) {//自底向上,最后一行已经赋值,不用遍历
    //自底向上计算,f[j] = a[i][j] + max(f[j], f[j + 1]);
    //要么取下面的值,要么取右下方的值,下方就是自己,而右下方相当于右边
        for (int j = 1; j <= i; j++) {//由于对于f[i,j]的计算会取到自己和右边的值,所以顺序,如果倒序就会取右边已经更新的点来更新
            f[j] = a[i][j] + max(f[j], f[j + 1]);
        }
    }
    cout << f[1] << endl;//第一个值就是最大值
    return 0;
}