分析

• 本题的考点动态规划。

• 分析如下：

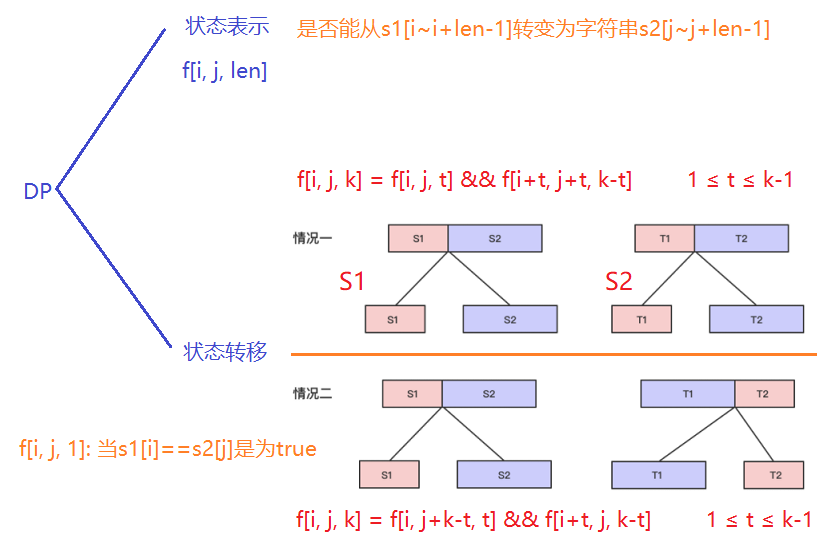
代码

• C++

class Solution {
public:
    bool isScramble(string s1, string s2) {

        int n = s1.size();
        // 初始化状态
        bool f[n][n][n + 1];
        memset(f, 0, sizeof f);
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                f[i][j][1] = (s1[i] == s2[j]);
        // 状态转移
        for (int len = 2; len <= n; len++)  // 遍历长度
            for (int i = 0; i + len - 1 < n; i++)  // 遍历s1的起点
                for (int j = 0; j + len - 1 < n; j++)  // 遍历s2的起点
                    for (int k = 1; k < len; k++) {
                        if (f[i][j][k] && f[i + k][j + k][len - k]) {
                            f[i][j][len] = true;
                            break;
                        }
                        if (f[i][j + len - k][k] && f[i + k][j][len - k]) {
                            f[i][j][len] = true;
                            break;
                        }
                    }
        return f[0][0][n];
    }
};

• Java

class Solution {
    public boolean isScramble(String s1, String s2) {

        char[] cs1 = s1.toCharArray(), cs2 = s2.toCharArray();
        int n = cs1.length;

        // 初始化状态
        boolean[][][] f = new boolean[n][n][n + 1];
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                f[i][j][1] = (cs1[i] == cs2[j]);

        // 状态转移
        for (int len = 2; len <= n; len++)
            for (int i = 0; i + len - 1 < n; i++)
                for (int j = 0; j + len - 1 < n; j++)
                    for (int k = 1; k < len; k++) {
                        if (f[i][j][k] && f[i + k][j + k][len - k]) {
                            f[i][j][len] = true;
                            break;
                        }
                        if (f[i][j + len - k][k] && f[i + k][j][len - k]) {
                            f[i][j][len] = true;
                            break;
                        }
                    }
        return f[0][0][n];
    }
}

时空复杂度分析

• 时间复杂度：$O(n^4)$，n为字符串的长度。

• 空间复杂度：$O(n^3)$。