分析
-
本题的考点:单调栈。
-
这一题可以看做Leetcode 0084 柱状图中的最大矩形的一个扩展,我们可以枚举每一行,将每一行看成一条基准线。对于某一行,看每个格子向上最多能到达的位置,当做这个位置的高度,然后就转化成了LC84的问题,如下图是转化过程(当枚举到第6行时,对应的各个柱子,红色的为对应的柱子):
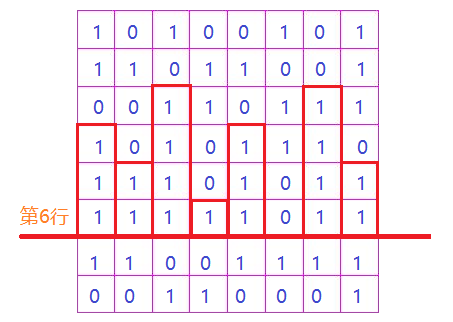
-
枚举每一行都会得到一个最大矩形的结果,这些结果中最大的一个就是答案。
-
另外还有一个问题,我们如何得到各个柱子的高度?,假设
h[i][j]表示第i行,第j列对应柱子的高度。这可以使用递推得到,即如果matrix[i][j] == 1的话,则h[i][j] = h[i - 1][j] + 1,否则h[i][j] = 0。 -
其实这个题还有一个扩展方向:如果让求最大的矩形,应该怎么办?对应题目:Leetcode 0221 最大正方形,本题这种解法也可以,需要在计算面积是判断是否为正方形。实际上LC221的正解是动态规划。
代码
- C++
class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
if (matrix.empty() || matrix[0].empty()) return 0;
int n = matrix.size(), m = matrix[0].size();
vector<vector<int>> h(n, vector<int>(m, 0));
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (matrix[i][j] == '1') {
if (i) h[i][j] = h[i - 1][j] + 1;
else h[i][j] = 1;
}
int res = 0;
for (int i = 0; i < n; i++) res = max(res, find(h[i]));
return res;
}
int find(vector<int>& h) {
int n = h.size();
stack<int> stk;
int l[n], r[n];
for (int i = 0; i < n; i++) {
while (stk.size() && h[stk.top()] >= h[i]) stk.pop();
if (stk.empty()) l[i] = -1;
else l[i] = stk.top();
stk.push(i);
}
stk = stack<int>(); // 清空栈,不存在clear()
for (int i = n - 1; i >= 0; i--) {
while (stk.size() && h[stk.top()] >= h[i]) stk.pop();
if (stk.empty()) r[i] = n;
else r[i] = stk.top();
stk.push(i);
}
int res = 0;
for (int i = 0; i < n; i++) res = max(res, h[i] * (r[i] - l[i] - 1));
return res;
}
};
- Java
class Solution {
public int maximalRectangle(char[][] matrix) {
if (matrix.length == 0 || matrix[0].length == 0) return 0;
int n = matrix.length, m = matrix[0].length;
int[][] h = new int[n][m];
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (matrix[i][j] == '1') {
if (i != 0) h[i][j] = h[i - 1][j] + 1;
else h[i][j] = 1;
}
int res = 0;
for (int i = 0; i < n; i++) res = Math.max(res, find(h[i]));
return res;
}
private int find(int[] h) {
int n = h.length;
Deque<Integer> stk = new ArrayDeque<>();
int[] l = new int[n], r = new int[n];
for (int i = 0; i < n; i++) {
while (!stk.isEmpty() && h[stk.peek()] >= h[i]) stk.pop();
if (stk.isEmpty()) l[i] = -1;
else l[i] = stk.peek();
stk.push(i);
}
stk.clear();
for (int i = n - 1; i >= 0; i--) {
while (!stk.isEmpty() && h[stk.peek()] >= h[i]) stk.pop();
if (stk.isEmpty()) r[i] = n;
else r[i] = stk.peek();
stk.push(i);
}
int res = 0;
for (int i = 0; i < n; i++) res = Math.max(res, h[i] * (r[i] - l[i] - 1));
return res;
}
}
时空复杂度分析
-
时间复杂度:$O(n \times m)$,
n、m为行数、列数。 -
空间复杂度:$O(n \times m)$。

