分析

• 本题的考点：单调栈。

• 对于每个柱子h[i]，我们求出其左边和右边小于h[i]且距离下标i最近的数据的下标left、right后，则以h[i]为高的柱子所能形成的矩形面积为$h[i] \times (right - left - 1)$。

• 我们可以使用单调栈寻找h[i]左边或右边小于h[i]的最近的数据的下标。

• 下面以求出数组中每个数左边第一个比它小的数为例讲解单调栈原理：

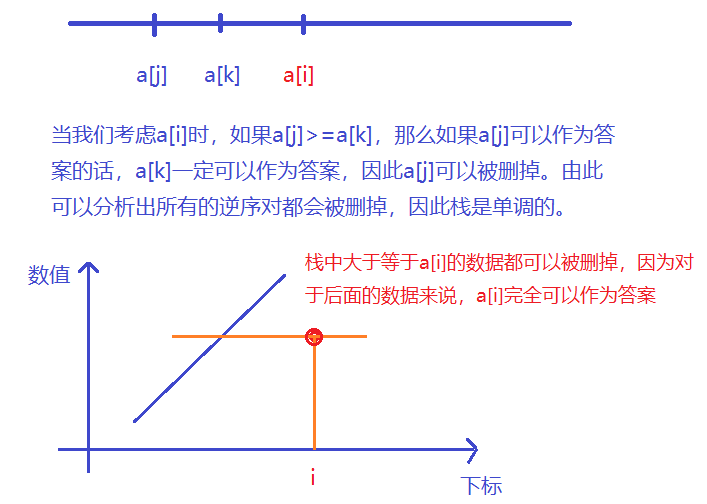
• 注意：单调栈中存储的元素对应的下标。

代码

• C++

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {

        int n = heights.size();
        vector<int> h(n + 2);
        h[0] = h[n + 1] = -1;  // 哨兵
        for (int i = 1; i <= n; i++) h[i] = heights[i - 1];

        stack<int> stk;
        int l[n + 1];  // l[i]:左边第一个小于h[i]的数据对应的下标
        int r[n + 1];  // r[i]:右边第一个小于h[i]的数据对应的下标

        stk.push(0);  // 将h[0]的下标放入栈，这样就不用判断栈是否为空了
        for (int i = 1; i <= n; i++) {
            while (h[stk.top()] >= h[i]) stk.pop();
            l[i] = stk.top();
            stk.push(i);
        }

        stk = stack<int>();  // 清空栈，不存在clear()
        stk.push(n + 1);  // 将h[n+1]的下标放入栈，这样就不用判断栈是否为空了
        for (int i = n; i; i--) {
            while (h[stk.top()] >= h[i]) stk.pop();
            r[i] = stk.top();
            stk.push(i);
        }

        int res = 0;
        for (int i = 1; i <= n; i++) res = max(res, h[i] * (r[i] - l[i] - 1));
        return res;
    }
};

• Java

class Solution {
    public int largestRectangleArea(int[] heights) {

        int n = heights.length;
        int[] h = new int[n + 2];
        h[0] = h[n + 1] = -1;  // 哨兵
        for (int i = 1; i <= n; i++) h[i] = heights[i - 1];

        Deque<Integer> stk = new ArrayDeque<>();
        int[] l = new int[n + 1], r = new int[n + 1];

        stk.push(0);  // 将h[0]的下标放入栈，这样就不用判断栈是否为空了
        for (int i = 1; i <= n; i++) {
            while (h[stk.peek()] >= h[i]) stk.pop();
            l[i] = stk.peek();
            stk.push(i);
        }

        stk.clear();
        stk.push(n + 1);  // 将h[n+1]的下标放入栈，这样就不用判断栈是否为空了
        for (int i = n; i > 0; i--) {
            while (h[stk.peek()] >= h[i]) stk.pop();
            r[i] = stk.peek();
            stk.push(i);
        }

        int res = 0;
        for (int i = 1; i <= n; i++) res = Math.max(res, h[i] * (r[i] - l[i] - 1));
        return res;
    }
}

时空复杂度分析

• 时间复杂度：$O(n)$，n为数组长度。

• 空间复杂度：$O(n)$。