题目描述

在一座城市里，你需要建 n 栋新的建筑。这些新的建筑会从 1 到 n 编号排成一列。

这座城市对这些新建筑有一些规定：

• 每栋建筑的高度必须是一个非负整数。
• 第一栋建筑的高度 必须 是 0。
• 任意两栋相邻建筑的高度差 不能超过 1。

除此以外，某些建筑还有额外的最高高度限制。这些限制会以二维整数数组 restrictions 的形式给出，其中 restrictions[i] = [id_i, maxHeight_i]，表示建筑 id_i 的高度 不能超过 maxHeight_i。

题目保证每栋建筑在 restrictions 中 至多出现一次，同时建筑 1 不会 出现在 restrictions 中。

请你返回 最高 建筑能达到的 最高高度。

样例

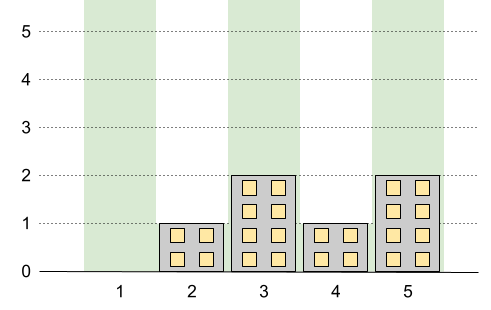
输入：n = 5, restrictions = [[2,1],[4,1]]
输出：2
解释：上图中的绿色区域为每栋建筑被允许的最高高度。
我们可以使建筑高度分别为 [0,1,2,1,2]，最高建筑的高度为 2。

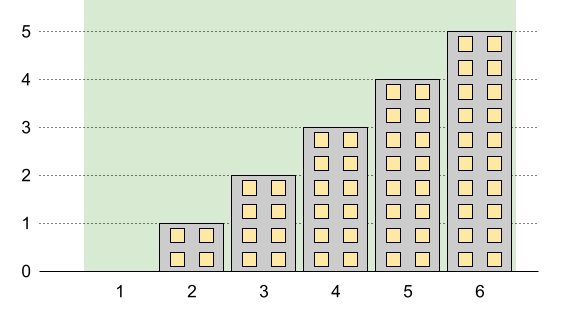
输入：n = 6, restrictions = []
输出：5
解释：上图中的绿色区域为每栋建筑被允许的最高高度。
我们可以使建筑高度分别为 [0,1,2,3,4,5]，最高建筑的高度为 5。

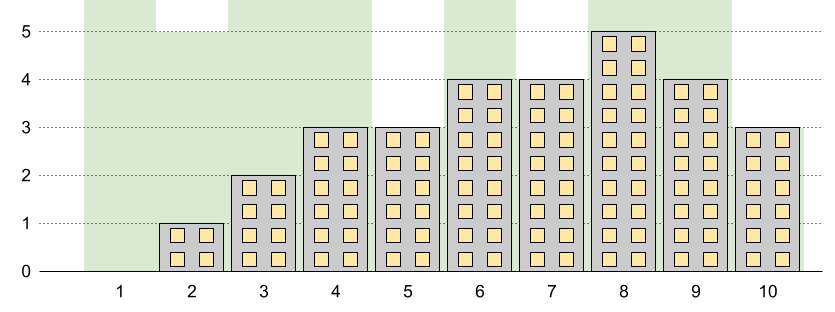
输入：n = 10, restrictions = [[5,3],[2,5],[7,4],[10,3]]
输出：5
解释：上图中的绿色区域为每栋建筑被允许的最高高度。
我们可以使建筑高度分别为 [0,1,2,3,3,4,4,5,4,3]，最高建筑的高度为 5。

限制

• 2 <= n <= 10^9
• 0 <= restrictions.length <= min(n - 1, 10^5)
• 2 <= id_i <= n
• id_i 是 唯一的。
• 0 <= maxHeight_i <= 10^9

算法

(贪心，数学) $O(n \log n)$

1. 将 restrictions 数组按照 $id_i$ 从小到大排序。
2. 算法分为两部分，第一部分先去掉较大 $id$ 影响到的较小的 $id$，第二部分在统计最大值。
3. 第一部分，如果我们发现有 $i$ 和 $j$，假设 $j < i$，满足 $height_j - (id_i - id_j) \ge height_i$，此时称作 $j$ 会影响到 $i$。这是因为 $j$ 受到 $i$ 的影响，不能够以 $height_j$ 作为参考限制，需要以 $height_i$ 作为参考限制。此时 $j$ 就失去了作用，可以去掉。
4. 使用单调栈过滤第一部分中无效的限制，然后进入第二部分。
5. 第二部分，分情况讨论最大值。初始时定义 $id_0 = 1$ 和 $height_0 = 0$。
6. 如果 $height_0 + (id_i - id_0) \le height_i$，则更新答案 $height_0 + (id_i - id_0)$，然后更新 $height_0 = height_0 + (id_i - id_0)$，$id_0 = id_i$。此时表示从上一次限制点，到此次的限制点，就算全部增长都达不到此次限制点的高度。
7. 另外一种情况，则必然存在某个点 $id_0 \le x \le id_i$ 为最高点，列方程求解：$height_0 + (x - id_0) - (id_i - x) = height_i$，解得 $x = (height_i + id_i - (height_0 - id_0)) / 2$。此时 $x$ 一定是合法解，更新答案，$height_0 + (x - id_0)$。更新 $height_0 = height_i$，$id_0 = id_i$。
8. 为了避免边界情况，在限制数组最后加上哨兵限制 [n, n - 1]。

时间复杂度

• 排序的时间复杂度为 $O(n \log n)$。
• 第一部分每个元素最多进栈一次，出栈一次，故时间复杂度为 $O(n)$。
• 第二部分，每个元素遍历一次。
• 故总时间复杂度为 $O(n \log n)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储单调栈。

C++ 代码

class Solution {
public:
    int maxBuilding(int n, vector<vector<int>>& restrictions) {
        restrictions.push_back({n, n - 1});
        sort(restrictions.begin(), restrictions.end());

        const int m = restrictions.size();

        vector<int> st;
        for (int i = 0; i < m; i++) {
            while (!st.empty() && restrictions[st.back()][1] - 
                (restrictions[i][0] - restrictions[st.back()][0]) >= restrictions[i][1])
                st.pop_back();

            st.push_back(i);
        }

        int ans = 0;
        int last_id = 1, last_height = 0;
        for (int i = 0; i < st.size(); i++) {
            int id = restrictions[st[i]][0], height = restrictions[st[i]][1];
            if (last_height + (id - last_id) <= height) {
                ans = max(ans, last_height + (id - last_id));

                last_height += id - last_id;
                last_id = id;
            } else {
                int x = (height + id - (last_height - last_id)) / 2;

                ans = max(ans, last_height + (x - last_id));

                last_height = height;
                last_id = id;
            }
        }

        return ans;
    }
};