题目描述
城堡守卫游戏的胜利条件为使恶魔无法从出生点到达城堡。游戏地图可视作 2*N 的方格图,记作字符串数组 grid,其中:
"."表示恶魔可随意通行的平地;"#"表示恶魔不可通过的障碍物,玩家可通过在 平地 上设置障碍物,即将"."变为"#"以阻挡恶魔前进;"S"表示恶魔出生点,将有大量的恶魔该点生成,恶魔可向上/向下/向左/向右移动,且无法移动至地图外;"P"表示瞬移点,移动到"P"点的恶魔可被传送至任意一个"P"点,也可选择不传送;"C"表示城堡。
然而在游戏中用于建造障碍物的金钱是有限的,请返回玩家最少需要放置几个障碍物才能获得胜利。若无论怎样放置障碍物均无法获胜,请返回 -1。
注意
- 地图上可能有一个或多个出生点。
- 地图上有且只有一个城堡。
样例
输入:grid = ["S.C.P#P.", ".....#.S"]
输出:3
解释:至少需要放置三个障碍物。
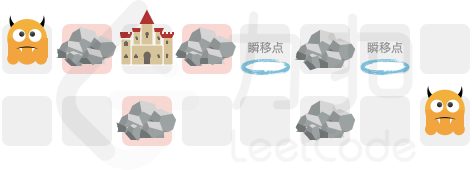
输入:grid = ["SP#P..P#PC#.S", "..#P..P####.#"]
输出:-1
解释:无论怎样修筑障碍物,均无法阻挡最左侧出生的恶魔到达城堡位置。

输入:grid = ["SP#.C.#PS", "P.#...#.P"]
输出:0
解释:无需放置障碍物即可获得胜利

输入:grid = ["CP.#.P.", "...S..S"]
输出:4
解释:至少需要放置 4 个障碍物,示意图为放置方法之一。

限制
grid.length == 22 <= grid[0].length == grid[1].length <= 10^4grid[i][j]仅包含字符"."、"#"、"C"、"P"、"S"。
算法1
(暴力最小割) $O(n^3)$
- 拆点建图,即每个点都拆成入点和出点。
- 如果是平地,则入点到出点的容量为 $1$。如果是城堡/恶魔/传送点,则入点到出点的容量为 $+\infty$。
- 平地/恶魔/传送点,其出点可以向周围的邻居入点连接容量为 $+\infty$ 的边。
- 定义一个额外的超级传送点
MOVE,其可以所有传送点的出点连接到MOVE容量为 $+\infty$ 的边,MOVE到所有传送点的入点连接容量为 $+\infty$ 的边。 - 新增源点,其连接到所有恶魔出生点的入点,容量为 $+\infty$。汇点则定义为城堡的出点。
- 用 dinic 或优化过的网络流量算法求以上网络的最大流(最小割)。
时间复杂度
- dinic 算法的时间复杂度为 $O(V^2E)$,这里 $E$ 和 $n$ 同阶,故总时间复杂度为 $O(n^3)$,但实际上远没有达到这个复杂度。
空间复杂度
- 需要 $O(n)$ 的额外空间存储网络流图和算法需要的数据结构。
C++ 代码
#define N 10010
#define INF 1000000000
struct Edge {
int to, flow, nxt;
};
class Solution {
private:
Edge e[N * 20];
int head[4 * N], counter;
int n, S, T;
int ch[4 * N];
void add(int x, int y, int c) {
int p = counter++;
e[p].to = y; e[p].flow = c; e[p].nxt = head[x]; head[x] = p;
p = counter++;
e[p].to = x; e[p].flow = 0; e[p].nxt = head[y]; head[y] = p;
}
int enter(int x, int y) {
return x * n + y;
}
int exit(int x, int y) {
return x * n + y + 2 * n;
}
void add_neighbors(int i, int j) {
const int dx[4] = {0, 1, 0, -1};
const int dy[4] = {1, 0, -1, 0};
for (int k = 0; k < 4; k++) {
int x = i + dx[k], y = j + dy[k];
if (x < 0 || x >= 2 || y < 0 || y >= n) continue;
add(exit(i, j), enter(x, y), INF);
}
}
bool bfs() {
memset(ch, -1, sizeof(ch));
ch[S] = 0;
queue<int> q;
q.push(S);
while(!q.empty()) {
int u = q.front();
q.pop();
for(int i = head[u]; i != -1; i = e[i].nxt) {
int v = e[i].to;
if(e[i].flow > 0 && ch[v] == -1) {
ch[v] = ch[u] + 1;
q.push(v);
}
}
}
if (ch[T] == -1) return false;
return true;
}
int dfs(int u, int r) {
if(u == T)
return r;
int t = 0;
for(int i = head[u]; i != -1 && r - t > 0; i = e[i].nxt) {
int v = e[i].to;
if(e[i].flow > 0 && ch[v] == ch[u] + 1) {
int b = dfs(v, min(e[i].flow, r - t));
e[i].flow -= b;
e[i^1].flow += b;
t += b;
}
}
if(t == 0) ch[u] = -1;
return t;
}
int dinic() {
int max_flow = 0;
while (bfs()) max_flow += dfs(S, INF);
if (max_flow == INF)
return -1;
return max_flow;
}
public:
int guardCastle(vector<string>& grid) {
memset(head, -1, sizeof(head));
counter = 0;
n = grid[0].size();
S = 4 * n;
int MOVE = 4 * n + 1;
for (int i = 0; i < 2; i++)
for (int j = 0; j < n; j++) {
if (grid[i][j] == '.') {
add(enter(i, j), exit(i, j), 1);
add_neighbors(i, j);
} else if (grid[i][j] == 'C') {
add(enter(i, j), exit(i, j), INF);
T = exit(i, j);
} else if (grid[i][j] == 'S') {
add(enter(i, j), exit(i, j), INF);
add(S, enter(i, j), INF);
add_neighbors(i, j);
} else if (grid[i][j] == 'P') {
add(enter(i, j), exit(i, j), INF);
add(exit(i, j), MOVE, INF);
add(MOVE, exit(i, j), INF);
add_neighbors(i, j);
}
}
return dinic();
}
};
算法2
(状态压缩动态规划) $O(n)$
- 枚举瞬移点的类型,共有三种:瞬移点既不和城堡连通,也不和恶魔连通;瞬移点和恶魔连通;瞬移点和城堡连通。
- 设状态 $f(i, s_j, s_k)$ 表示考虑了前 $i$ 列时,第一行的状态为 $s_j$,第二行的状态为 $s_k$ 时需要放置的最少障碍数。其中,$s_j$ 与 $s_k$ 保证是合法的。
- 状态 $s$ 有五种,按顺序分别对应了题面中五种类型。判断第一行与第二行的状态合法需要把握几个原则:恶魔/城堡会移动到空格上(所以恶魔与空格是不合法的);恶魔不能遇到城堡;如果瞬移点是空,则不能与恶魔或城堡连通。这些原则同样适用于转移时的合法性判断。
- 初始时,$f(0, 1, 1) = 0$,其余为 $+\infty$。
- 对于第 $i$ 列,枚举第 $i - 1$ 列的状态 $s_j$ 和 $s_k$,与第 $i$ 列的真实值 $x$ 和 $y$ 进行转移。
- 最终答案为 $f(n, s_j, s_k)$。
时间复杂度
- 状态数为 $O(n)$,转移数常数,故总时间复杂度为 $O(n)$。
空间复杂度
- 需要 $O(n)$ 的额外空间存储状态。
- 可以通过滚动数组优化空间为常数。
C++ 代码
#define N 10010
class Solution {
private:
int f[N][5][5];
bool check(int x, int y) {
return !(x >= 2 && y >= 2 && x != y);
}
void trans(int i, int j, int k, int p, int x, int y, int cost) {
if (x == 0 && j == 2) x = 2; // 两列状态的同步(恶魔/城堡到空格)
if (x == 0 && j == 4) x = 4;
if (y == 0 && k == 2) y = 2;
if (y == 0 && k == 4) y = 4;
if (x == 0 && y == 2) x = 2; // 第 i 列状态的同步(恶魔/城堡到空格)
if (x == 0 && y == 4) x = 4;
if (y == 0 && x == 2) y = 2;
if (y == 0 && x == 4) y = 4;
if (!check(j, x) || !check(k, y) || !check(x, y)) // 合法性判断
return;
f[i][x][y] = min(f[i][x][y], f[i - 1][j][k] + cost); // 转移
}
void solve(int i, int j, int k, int p, int x, int y) {
if (x == 3) { // 翻译瞬移点
if (p == 1) x = 2;
else if (p == 2) x = 4;
}
if (y == 3) { // 翻译瞬移点
if (p == 1) y = 2;
else if (p == 2) y = 4;
}
trans(i, j, k, p, x, y, 0);
if (x == 0) trans(i, j, k, p, 1, y, 1);
if (y == 0) trans(i, j, k, p, x, 1, 1);
if (x == 0 && y == 0) trans(i, j, k, p, 1, 1, 2);
}
public:
int guardCastle(vector<string>& grid) {
unordered_map<char, int> h;
h['.'] = 0; h['#'] = 1; h['S'] = 2; h['P'] = 3; h['C'] = 4;
const int n = grid[0].size();
const int INF = 1000000000;
int ans = INF;
for (int p = 0; p < 3; p++) {
for (int i = 0; i <= n; i++)
for (int j = 0; j < 5; j++)
for (int k = 0; k < 5; k++)
f[i][j][k] = INF;
f[0][1][1] = 0;
for (int i = 1; i <= n; i++)
for (int j = 0; j < 5; j++)
for (int k = 0; k < 5; k++)
if (f[i - 1][j][k] < INF)
solve(i, j, k, p, h[grid[0][i - 1]], h[grid[1][i - 1]]);
for (int j = 0; j < 5; j++)
for (int k = 0; k < 5; k++)
ans = min(ans, f[n][j][k]);
}
if (ans == INF)
return -1;
return ans;
}
};

