分析

• 本题的考点：高精度乘法。

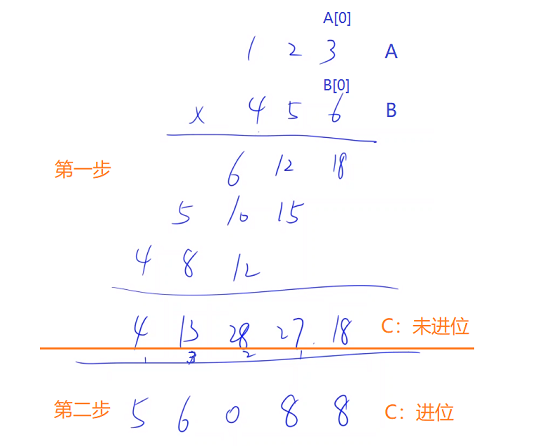
• 首先我们将数据存储到数组A、B中，其中A[0]、 B[0]存储的数字的个位，结果存储到C数组中，分为两步：

（1）不考虑进位直接将$A[i] \times B[j]$的结果存到$C[i + j]$中；

（2）处理C中的进位。如下图：$123 \times 456$：

代码

• C++

class Solution {
public:
    string multiply(string num1, string num2) {

        vector<int> A, B;
        int n = num1.size(), m = num2.size();
        for (int i = n - 1; i >= 0; i--) A.push_back(num1[i] - '0');
        for (int i = m - 1; i >= 0; i--) B.push_back(num2[i] - '0');

        // (1) 不考虑进位，将结果存入C中
        vector<int> C(n + m);
        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
                C[i + j] += A[i] * B[j];
        // (2) 考虑进位
        for (int i = 0, t = 0; i < C.size(); i++) {
            t += C[i];
            C[i] = t % 10;
            t /= 10;
        }

        // 处理输出
        int k = C.size() - 1;
        while (k && C[k] == 0) k--;
        string res;
        while (k >= 0) res += C[k--] + '0';
        return res;
    }
};

• Java

class Solution {
    public String multiply(String num1, String num2) {

        int n = num1.length(), m = num2.length();
        int[] A = new int[n], B = new int[m];
        for (int i = n - 1; i >= 0; i--) A[n - 1 - i] = num1.charAt(i) - '0';
        for (int i = m - 1; i >= 0; i--) B[m - 1 - i] = num2.charAt(i) - '0';

        // (1) 不考虑进位，将结果存入C中
        int[] C = new int[n + m];
        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
                C[i + j] += A[i] * B[j];
        // (2) 考虑进位
        for (int i = 0, t = 0; i < C.length; i++) {
            t += C[i];
            C[i] = t % 10;
            t /= 10;
        }

        // 处理输出
        int k = C.length - 1;
        while (k > 0 && C[k] == 0) k--;
        StringBuilder sb = new StringBuilder();
        while (k >= 0) sb.append((char)(C[k--] + '0'));
        return sb.toString();
    }
}

时空复杂度分析

• 时间复杂度：$O(n \times m)$，n为num1的长度，m为num2的长度。

• 空间复杂度：$O(n + m)$，n为num1的长度，m为num2的长度。