分析

• 本题的考点：二分。
• 二分的本质是二段性。
• 本题使用两次二分：（1）二分出旋转点的位置；（2）第二次二分出答案。关键是第一次二分，如下图：

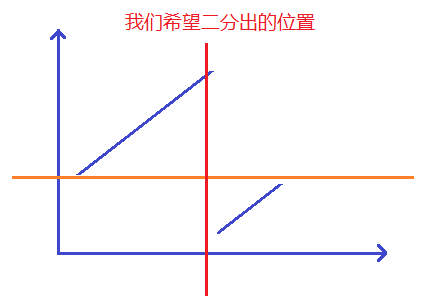
• 我们可以发现左右两部分具有两段性，左边元素全部$\ge nums[0]$，右边的元素$<nums[0]$。据此可以二分出分界点。

• 之后判断我们需要寻找的目标值target和nums[0]之间的关系，如果$target \ge nums[0]$，则在第一段中第二次二分，否则在另一半二分。

代码

• C++

class Solution {
public:
    int search(vector<int>& nums, int target) {

        // 二分分界点
        int l = 0, r = nums.size() - 1;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (nums[mid] >= nums[0]) l = mid;
            else r = mid - 1;
        }
        // 判断target在哪一段中
        if (target >= nums[0]) l = 0;
        else l = r + 1, r = nums.size() - 1;
        // 二分出答案
        while (l < r) {
            int mid = l + r >> 1;
            if (nums[mid] >= target) r = mid;
            else l = mid + 1;
        }

        if (nums[r] == target) return r;
        return -1;
    }
};

• Java

class Solution {
    public int search(int[] nums, int target) {

        // 二分分界点
        int l = 0, r = nums.length - 1;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (nums[mid] >= nums[0]) l = mid;
            else r = mid - 1;
        }
        // 判断target在哪一段中
        if (target >= nums[0]) l = 0;
        else {
            l = r + 1; r = nums.length - 1;
        }
        // 二分出答案
        while (l < r) {
            int mid = l + r >> 1;
            if (nums[mid] >= target) r = mid;
            else l = mid + 1;
        }

        if (nums[r] == target) return r;
        return -1;
    }
}

时空复杂度分析

• 时间复杂度：$O(log(n)$，n为数组长度。

• 空间复杂度：$O(1)$。