分析

• 本题的考点：栈。

• 首先，对于只含有小括号的序列，我们应该清楚序列时合法的，需要满足两个条件：

（1）左右括号数量相等；

（2）任意前缀中左括号数量一定大于等于右括号数量。

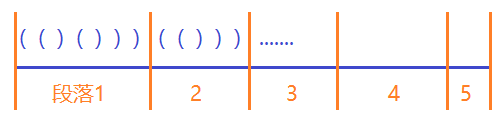
• 第一步我们应该将整个括号序列分段：从左向右找到第一个前缀中右括号数量大于左括号数量的位置，这个前缀是第一个分段；然后继续对后面的序列进行这样的操作，这样我们可以将整个序列划分成多个分段，可以证明最长的有效括号的不会跨越多个段，只能在段内，如下图：

• 下面证明最长的有效括号的不会跨越多个段，可以使用反证法：

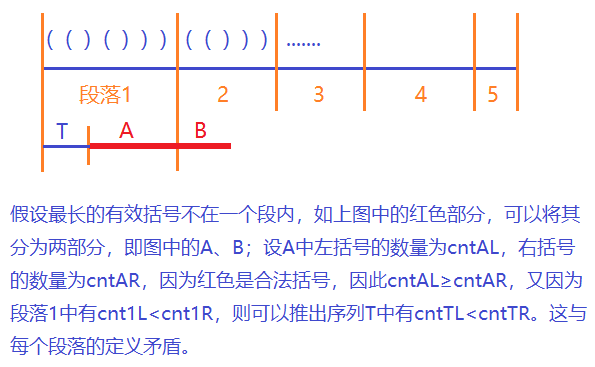
• 之后我们可以使用一个栈记录所有的左括号下标，遇到左括号直接将其下标入栈。

• 遇到右括号分为两种情况讨论：

（1）如果栈非空，将栈顶元素出队，如果出队之后栈非空则此时栈顶元素的下一个位置到当前位置是有效括号，如果栈为空则从该段的起始位置到当前位置是有效括号；

（2）如果栈为空，说明遇到右括号但是没有可以匹配的左括号，该段结束，进行下一段。

代码

• C++

class Solution {
public:
    int longestValidParentheses(string s) {

        stack<int> stk;

        int res = 0;
        for (int i = 0, start = -1; i < s.size(); i++) {  // start为每段起始位置的前一个位置
            if (s[i] == '(') stk.push(i);
            else {  // 说明是右括号
                if (stk.size()) {  // (1) 栈非空
                    stk.pop();
                    if (stk.size()) res = max(res, i - stk.top());
                    else res = max(res, i - start);
                } else {  // (2) 栈空, 说明遇到右括号但是没有可以匹配的左括号，该段结束，进行下一段
                    start = i;
                }
            }
        }
        return res;
    }
};

• Java

class Solution {
    public int longestValidParentheses(String s) {

        Deque<Integer> stk = new ArrayDeque<>();

        char[] cs = s.toCharArray();
        int res = 0;
        for (int i = 0, start = -1; i < cs.length; i++) {  // start为每段起始位置的前一个位置
            if (cs[i] == '(') stk.push(i);
            else {  // 说明是右括号
                if (!stk.isEmpty()) {  // (1) 栈非空
                    stk.pop();
                    if (!stk.isEmpty()) res = Math.max(res, i - stk.peek());
                    else res = Math.max(res, i - start);
                } else {  // (2) 栈空, 说明遇到右括号但是没有可以匹配的左括号，该段结束，进行下一段
                    start = i;
                }
            }
        }
        return res;
    }
}

时空复杂度分析

• 时间复杂度：$O(n)$，n为字符串s的长度。

• 空间复杂度：$O(n)$，n为字符串s的长度。