代码
#include <algorithm>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 3e2 + 10;
int n, m;
int g[N][N];
int f[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int dp(int x, int y)
{
int& v = f[x][y];
if (v != -1) {
return v;
}
v = 1;
for (int i = 0; i < 4; i++) {
int a = x + dx[i], b = y + dy[i];
if (a >= 1 && a <= n && b >= 1 && b <= m && g[x][y] > g[a][b]) {
v = max(v, dp(a, b) + 1);
}
}
return v;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> g[i][j];
}
}
memset(f, -1, sizeof f);
int res = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
res = max(res, dp(i, j));
}
}
cout << res << endl;
return 0;
}


int& v = f[x][y];引用没看到,T了一发QAQ给后来的人提个醒
我一般习惯
return f[x][y] = v;大佬头像也太好看了,每次一点题解都能很清楚地看到你
谢谢!
大佬, 我有个问题 什么时候 是用正常的dp递推 什么时候采用记忆化搜索? 是根据当前问题的子问题 来看?
如果子问题 好求出来 就像是 数字三角形 就用正常递推就行 这个的子问题 不太好求 所以才用的 dfs 求子问题 是吧?
记忆化搜索只是dp的一种实现方式,记忆化搜索可以实现然而普通递推不能实现的问题(或实现起来非常麻烦的问题)就用记忆化搜索, 比如这题
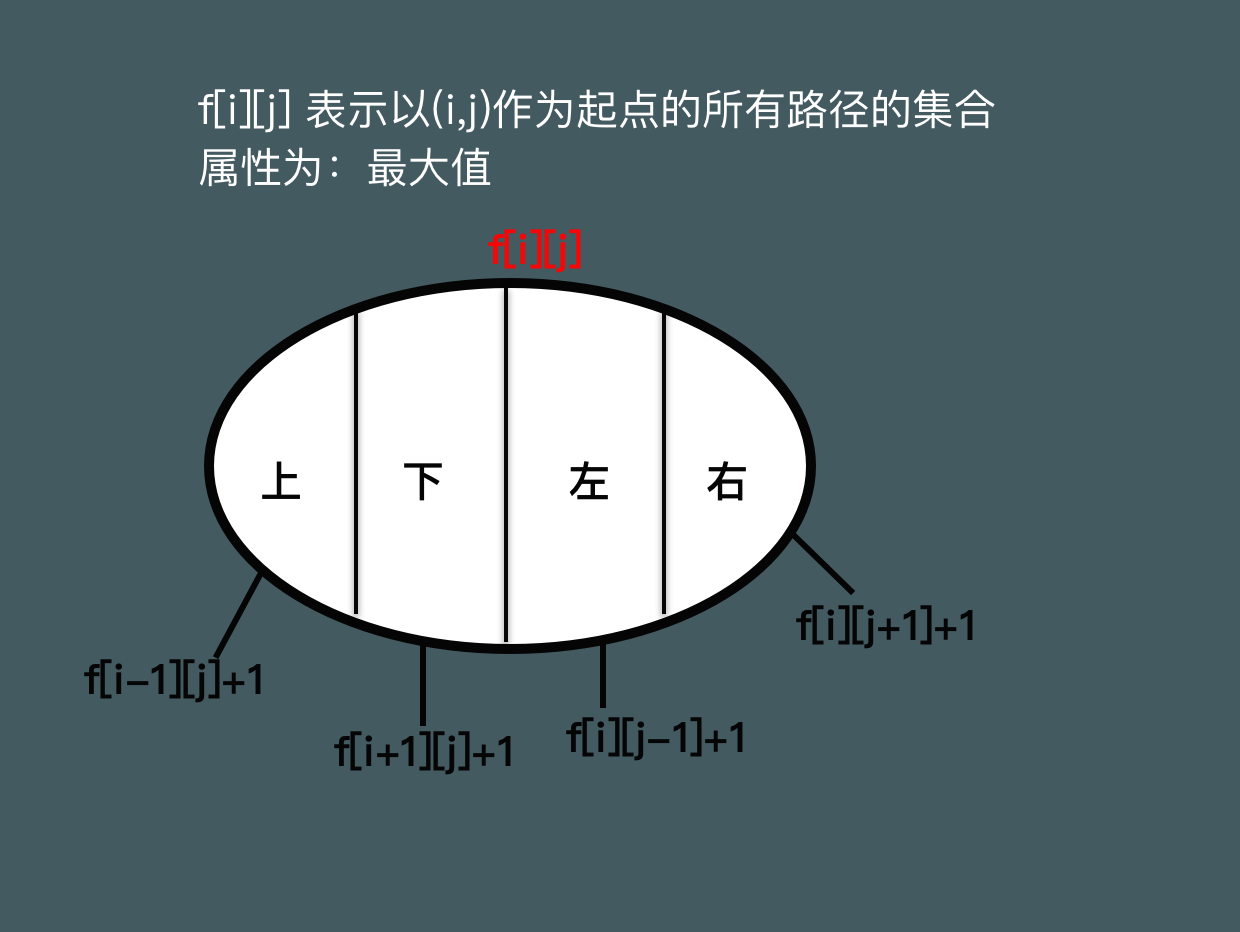
我们假设f[i][j]表示滑到坐标(i,j)所能滑到的最长长度。那么对于状态f[i][j]而言,它可以由f[i-1][j],f[i][j-1],f[i+1][j],f[i][j+1]四个状态推得,然而我们使用普通的递推(两个for)只能得到上、左两个方向的状态,右、下两个方向的状态却无从得知,因此使用递推就不能满足我们的要求,如果再补上两个for覆盖右、下状态,那么时间复杂度就变为了N^4,很明显会TLE
嗯啊 多谢了😄