分析

• 本题的考点：哈希表、滑动窗口、字符串哈希。

• 首先约定一些常数：n=s.size(), m=words.size(), w=word[i].size()。哈希表tot记录words中每个单词出现的次数。

• 我们可以枚举由words组成的子串在s中的起始位置，因为words中的单词长度为w，因此起点位置对w取模，可以分为w个同余类，即0~w-1，如下图，每行是一个同余类：

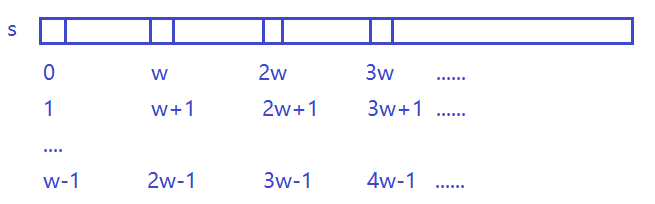
• 对于每个同余类，即确定了子串的起点，我们采用滑动窗口，滑窗中的单词采用哈希表wd记录，如果滑窗中元素等于m，则判断滑窗中的单词和words中的单词是否完全相同，如果完全相同，则得到一个答案，滑动窗口向后移动w个字母，然后将这个新单词插入wd中，滑窗最前面的单词需要被删除，下面以模0同余类演示一下滑窗的操作：

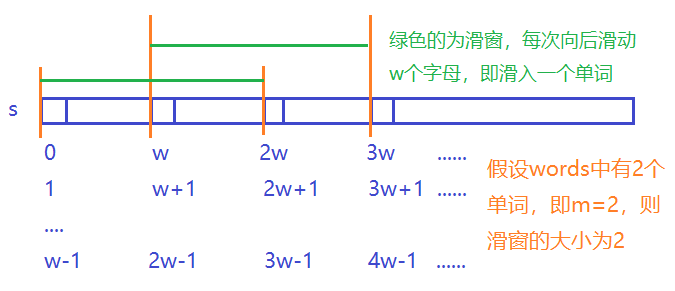
• 那么如何确定滑窗wd中的单词和tot中的单词全部一模一样呢，我们可以使用一个变量cnt记录相同单词的数量，如果一个单词在tot中出现多次，比如出现3次，但是在滑窗中出现4次，但cnt只能将该单词加3次，当cnt == m时，说明窗wd中的单词和tot中的单词一模一样，得到一个答案。

• 每个同余类有$\frac{n}{w}$个单词，每操作一个单词，即向wd中插入一个单词计算量是$w$，因此每个同余类计算量为$O(\frac{n}{w} \times w)=O(n)$量级的，一共w组，因此总的时间复杂度为$O(n \times w)$的。

• 这里可以对向wd中插入一个单词进行优化，使得插入的计算量为$O(1)$，从而总体时间复杂度降为$O(n)$。采用的方式是字符串哈希（字符串哈希）。

代码

• C++

class Solution {
public:
    typedef unsigned long long ULL;

    static const int P = 131;

    ULL get(ULL h[], ULL p[], int l, int r) {
        return h[r] - h[l - 1] * p[r - l + 1];
    }

    vector<int> findSubstring(string s, vector<string> &words) {

        vector<int> res;
        if (words.empty()) return res;
        int n = s.size(), m = words.size(), w = words[0].size();

        // 求s的字符串哈希结果, 从1开始，即h[1]=s[0], 后面求hash值的时候要加上一个偏移量
        ULL h[n + 10], p[n + 10];  // p[i] = 10 ^ i
        h[0] = 0, p[0] = 1;
        for (int i = 1; i <= n; i++) {
            h[i] = h[i - 1] * P + s[i - 1];
            p[i] = p[i - 1] * P;
        }

        // 统计words中每个单词出现的次数
        unordered_map<ULL, int> tot;
        for (auto &word : words) {
            ULL t = 0;
            for (auto c : word) t = t * P + c;
            tot[t]++;
        }

        for (int i = 0; i < w; i++) {
            unordered_map<ULL, int> wd;  // windows的缩写
            int cnt = 0;
            for (int j = i; j + w - 1 < n; j += w) {  // 滑动窗口
                // 滑窗为[j-m*w, j)
                // 每次滑入[j, j+w-1], 滑出[j-m*w, j-m*w-1]
                if (j >= i + m * w) {
                    // 获取单词s[j - m * w, j - m * w + w - 1]对应的哈希值
                    ULL hash = get(h, p, j - m * w + 1, j - m * w + w);
                    wd[hash]--;
                    if (wd[hash] < tot[hash]) cnt--;
                }
                // 获取单词s[j, j + w - 1]对应的哈希值
                ULL hash = get(h, p, j + 1, j + w);
                wd[hash]++;
                if (wd[hash] <= tot[hash]) cnt++;
                if (cnt == m) res.push_back(j - (m - 1) * w);
            }
        }
        return res;
    }
};

• Java

// Java这里不演示使用字符串哈希了
class Solution {
    public List<Integer> findSubstring(String s, String[] words) {

        List<Integer> res = new ArrayList<>();
        if (s.length() == 0) return res;
        int n = s.length(), m = words.length, w = words[0].length();
        HashMap<String, Integer> tot = new HashMap<>();
        for (String word : words) tot.put(word, tot.getOrDefault(word, 0) + 1);

        for (int i = 0; i < w; i++) {
            HashMap<String, Integer> wd = new HashMap<>();
            int cnt = 0;
            for (int j = i; j + w - 1 < n; j += w) {  // 滑动窗口
                // 滑窗为[j-m*w, j)
                // 每次滑入[j, j+w), 滑出[j-m*w, j-m*w+w)
                if (j >= i + m * w) {
                    String word = s.substring(j - m * w, j - (m - 1) * w);
                    wd.put(word, wd.getOrDefault(word, 0) - 1);
                    if (wd.get(word) < tot.getOrDefault(word, 0)) cnt--;
                }
                String word = s.substring(j, j + w);
                wd.put(word, wd.getOrDefault(word, 0) + 1);
                if (wd.get(word) <= tot.getOrDefault(word, 0)) cnt++;
                if (cnt == m) res.add(j - (m - 1) * w);
            }
        }
        return res;
    }
}

时空复杂度分析

• 时间复杂度：使用字符串哈希：$O(n)$，n为s的长度。不使用字符串哈希：$O(n \times w)$，n为s的长度，w为word[0]长度。

• 空间复杂度：$O(m)$，m为数组words的长度。