题目描述

用KMP算法在字符串里寻找模式串

算法

KMP

时间复杂度:$O(nlogn)$

KMP算法精髓:

当模式串在第n位不匹配时
模式串的前n-1位字符串 == 文本串当前匹配点的前n-1位
因此可以利用模式串的前n-1位来确定偏移量

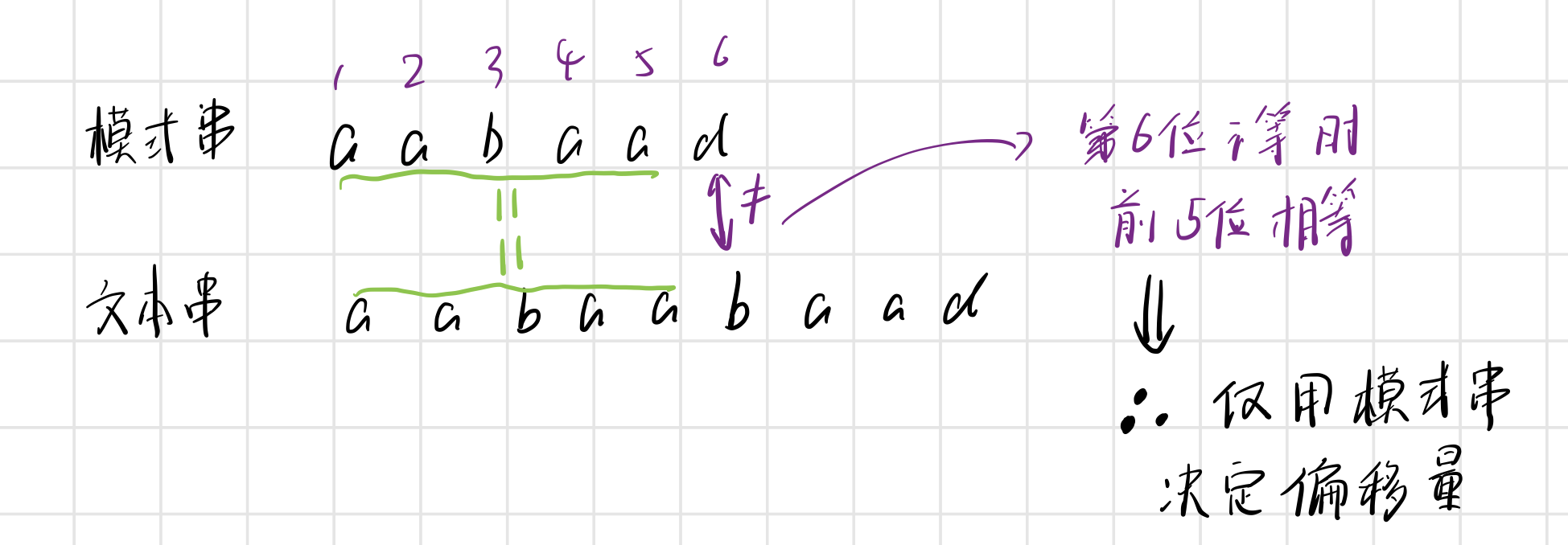
如何根据模式串求偏移量

如何求偏移量,就是next数组干的活了
首先要了解字符串的前后缀

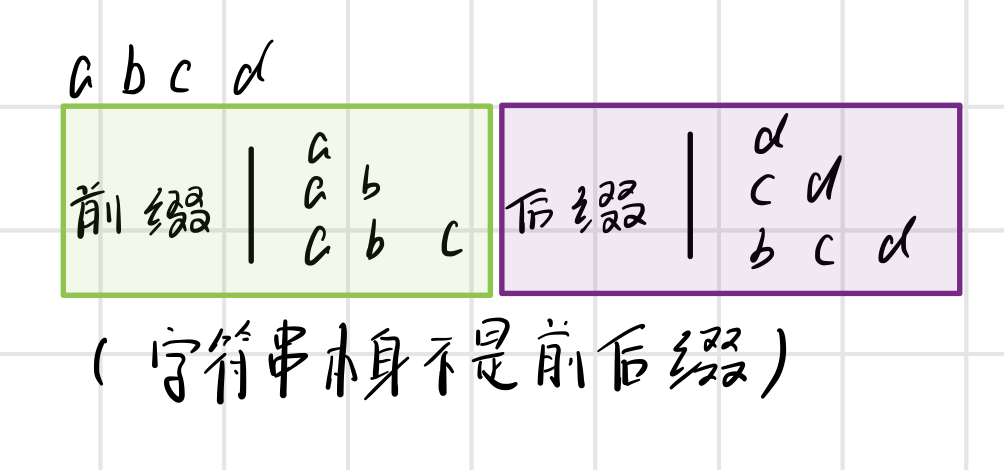
最大相等前后缀意味着,下一次匹配可以把
n-1子串的前缀(模式串中)与n-1子串的后缀(文本串中)相对应,获得最大相匹配的位数

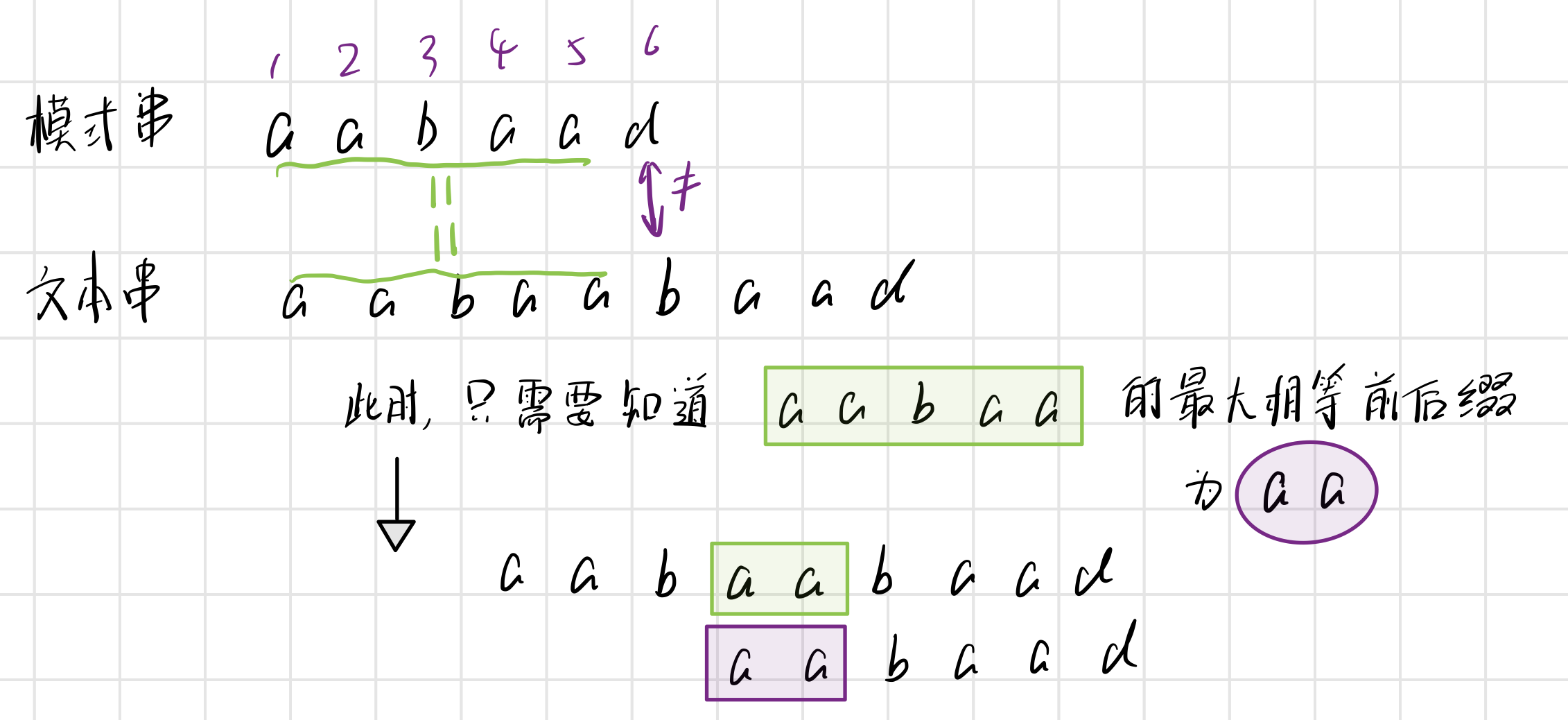
根据上面的分析可以求得next数组
由于此时,第i位不匹配时,我们要从next[i-1]处寻找,因此,很多时候,将前缀表全部-1

//求next数组
void findnext(int* next, const string& s){
    int j = -1;
    next[0] = j;
    for(int i = 1; i < s.size(); i++){
        while(j>=0 and s[j+1] != s[i]){//因为将next数组-1,因此此处为j+1
            j = next[j];
        }
        if(s[i]==s[j]){
            j++;
        }
        next[i] = j;
    }
}

C++ 代码

void findnext(int* next, const string& s){
    int j = -1;
    next[0] = j;
    for(int i = 1; i < s.size(); i++){
        while(j>=0 and s[i]!= s[j+1]){
            j = next[j];
        }
        if(s[j+1]==s[i]){
            j++;
        }
        next[i] = j;
    }
}

int main (){
    int n,m;
    string pattern, source;
    cin >> n;
    cin >> pattern;
    cin >> m;
    cin >> source;
    int next[n];
    findnext(next, pattern);
    int j = -1;
    for(int i = 0; i < s.size(), i++){
        while(j>=0 and s[i]!=s[j+1]){
            j = next[j];
        }
        if(s[j+1]==s[i]){
            j++;
        }
        if(j==s.size()-1){
            cout<< i-n+1 <<" ";
        }

    }
    return 0;
}