分析

• 本题的考点：二维前缀和、暴力枚举。

• 为了快速求出每个矩形中数据之和，可以使用二维前缀和技巧，前缀和中的坐标一般都是从1开始的。

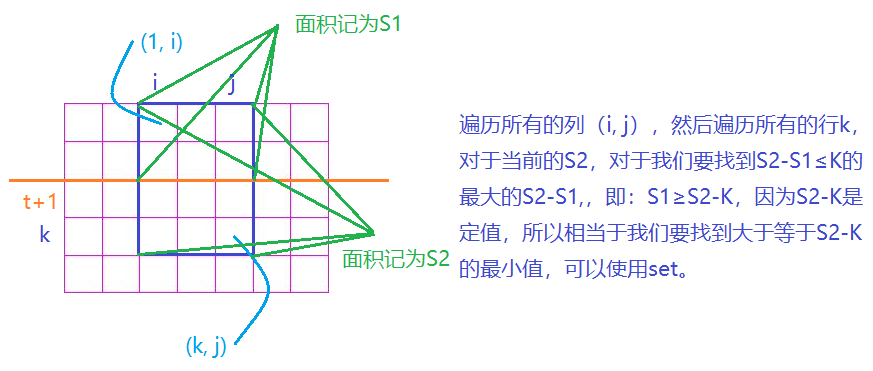
代码

• C++

class Solution {
public:
    vector<vector<int>> sum;  //  二维前缀和

    int get(int x1, int y1, int x2, int y2) {
        return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
    }

    int maxSumSubmatrix(vector<vector<int>> &w, int K) {

        int n = w.size(), m = w[0].size();
        sum = vector<vector<int>>(n + 1, vector<int>(m + 1));
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + w[i - 1][j - 1];

        int res = INT_MIN;
        for (int i = 1; i <= m; i++)
            for (int j = i; j <= m; j++) {
                set<int> S;
                S.insert(0);
                for (int k = 1; k <= n; k++) {
                    int s2 = get(1, i, k, j);
                    auto s1 = S.lower_bound(s2 - K);
                    if (s1 != S.end()) res = max(res, s2 - *s1);
                    S.insert(s2);
                }
            }
        return res;
    }
};

• Java

class Solution {
    int[][] sum;  // 二维前缀和

    private int get(int x1, int y1, int x2, int y2) {
        return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
    }

    public int maxSumSubmatrix(int[][] w, int K) {

        int n = w.length, m = w[0].length;
        sum = new int[n + 1][m + 1];
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + w[i - 1][j - 1];

        int res = Integer.MIN_VALUE;
        for (int i = 1; i <= m; i++)
            for (int j = i; j <= m; j++) {
                TreeSet<Integer> S = new TreeSet<>();
                S.add(0);
                for (int k = 1; k <= n; k++) {
                    int s2 = get(1, i, k, j);
                    Integer s1 = S.ceiling(s2 - K);
                    if (s1 != null) res = Math.max(res, s2 - s1);
                    S.add(s2);
                }
            }
        return res;
    }
}

时空复杂度分析

• 时间复杂度：$O(m^2 \times n \times log(n))$，n、m分别为行数、列数。因为有三重循环，再加上在set中查找是$log(n)$的复杂度，因此时间复杂度为$O(m^2 \times n \times log(n))$。

• 空间复杂度：$O(n \times m)$。