分析

• 本题的考点：二分。

• 这里将nums1、nums2分别记为A、B。对于给定的数组A、B，我们要找到这两个数组中的中位数，我们考虑一个更加一般的问题，如何找到第k小的数据。

• 假设我们需要找到A[i...]和B[j...]这两个数组的第k小的数据，则我们可以比较 $A[i+\lfloor \frac{k}{2}\rfloor-1]$ 和 $B[j+\lfloor \frac{k}{2}\rfloor-1]$ 的大小，则会存在三种情况：

（1） $A[i+\lfloor \frac{k}{2}\rfloor-1] \le B[j+\lfloor \frac{k}{2}\rfloor-1]$ ：说明 $A[i…i+\lfloor \frac{k}{2}\rfloor-1]$ 都不可能是第k小的数，这是因为即使$B[j…j+\lfloor \frac{k}{2}\rfloor-2]$都小于$A[i+\lfloor \frac{k}{2}\rfloor-1]$的话，$A[i+\lfloor \frac{k}{2}\rfloor-1]$也只是第k-1小的数，因此可以被删除；

（2） $A[i+\lfloor \frac{k}{2}\rfloor-1] > B[j+\lfloor \frac{k}{2}\rfloor-1]$ ：说明 $B[j…j+\lfloor \frac{k}{2}\rfloor-1]$ 都不可能是第k小的数，同理也可以被删除；

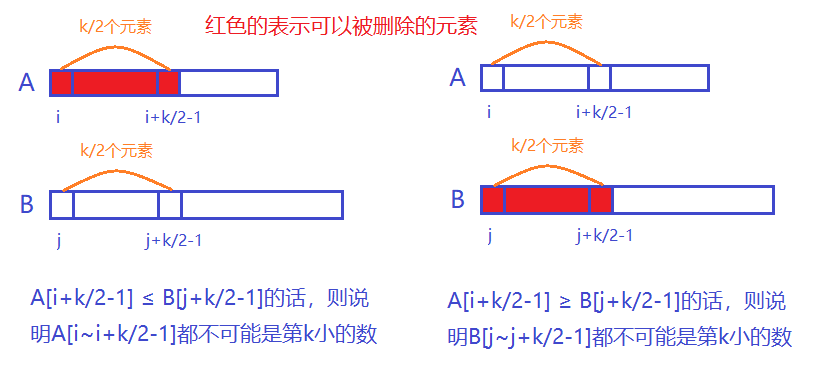
• 下面的代码中让：$newI = i+\lfloor \frac{k}{2}\rfloor-1$，$newJ = j+\lfloor \frac{k}{2}\rfloor-1$。

代码

• C++

class Solution {
public:
    double findMedianSortedArrays(vector<int>& A, vector<int>& B) {

        int n = A.size() + B.size();
        if (n % 2) return get(A, B, n / 2 + 1);
        else {
            int l = get(A, B, n / 2);
            int r = get(A, B, n / 2 + 1);
            return (l + r) / 2.0;
        }
    }

    // 在两个有序数组 A 和 B 中获取第k小(从1开始)的数据
    int get(vector<int> A, vector<int> B, int k) {

        int i = 0, j = 0;  // 当前考察的区间 nums1[i...], nums2[j...]
        while (true) {
            // 考虑各种边界情况
            if (i == A.size()) return B[j + k - 1];
            if (j == B.size()) return A[i + k - 1];
            if (k == 1) return min(A[i], B[j]);

            int newI = min(i + k / 2, (int)A.size()) - 1;
            int newJ = min(j + k / 2, (int)B.size()) - 1;
            if (A[newI] <= B[newJ]) {
                k -= (newI - i + 1);  // 此时应该删除A[i...newI]
                i = newI + 1;
            } else {
                k -= (newJ - j + 1);  // 此时应该删除B[j...newJ]
                j = newJ + 1;
            }
        }
    }
};

• Java

class Solution {
    public double findMedianSortedArrays(int[] A, int[] B) {

        int n = A.length + B.length;
        if (n % 2 != 0) {
            return get(A, B, n / 2 + 1);
        } else {
            int l = get(A, B, n / 2);
            int r = get(A, B, n / 2 + 1);
            return (l + r) / 2.0;
        }
    }

    // 在两个有序数组 A 和 B 中获取第k小(从1开始)的数据
    private int get(int[] A, int[] B, int k) {

        int i = 0, j = 0;  // 当前考察的区间 nums1[i...], nums2[j...]
        while (true) {
            // 考虑各种边界情况
            if (i == A.length) return B[j + k - 1];
            if (j == B.length) return A[i + k - 1];
            if (k == 1) return Math.min(A[i], B[j]);

            int newI = Math.min(i + k / 2, A.length) - 1;
            int newJ = Math.min(j + k / 2, B.length) - 1;
            if (A[newI] <= B[newJ]) {
                k -= (newI - i + 1);  // 此时应该删除A[i...newI]
                i = newI + 1;
            } else {
                k -= (newJ - j + 1);  // 此时应该删除B[j...newJ]
                j = newJ + 1;
            }
        }
    }
}

时空复杂度分析

• 时间复杂度：$O(log(n+m))$，n、m为两个数组的长度。这是因为我们每次会让k减少一半。

• 空间复杂度：$O(1)$。