题目描述

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为非负值。

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。

输入格式
第一行包含整数 n 和 m。

接下来 m 行每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式
输出一个整数，表示 1 号点到 n 号点的最短距离。

如果路径不存在，则输出 −1。

数据范围
1≤n,m≤1.5×105,
图中涉及边长均不小于 0，且不超过 10000。

样例

输入样例：
3 3
1 2 2
2 3 1
1 3 4
输出样例：
3

朴素Dij $\mathrm{O}(\mathrm{n^2})$

先吐槽一下Dijkstra这个人名字里面包含ijk最常用的三个循环变量,不会就是因为这个人写的算法所以后人都用ijk作为循环下标吧

算法思路:

dist[i]记录i点到起点的距离,S集合(已经确定最短距离的点的集合)

1. 初始化距离矩阵 初始点到初始点距离为0,其余赋值为无穷(从几号点开始就赋值几号点为0,本题从1号点开始)
2. for(i:1~n)遍历所有的点
   1. 找到不在S集合中距离起点最近的点t
   2. 把t加入到S中,用t点到其他点的距离更新dist

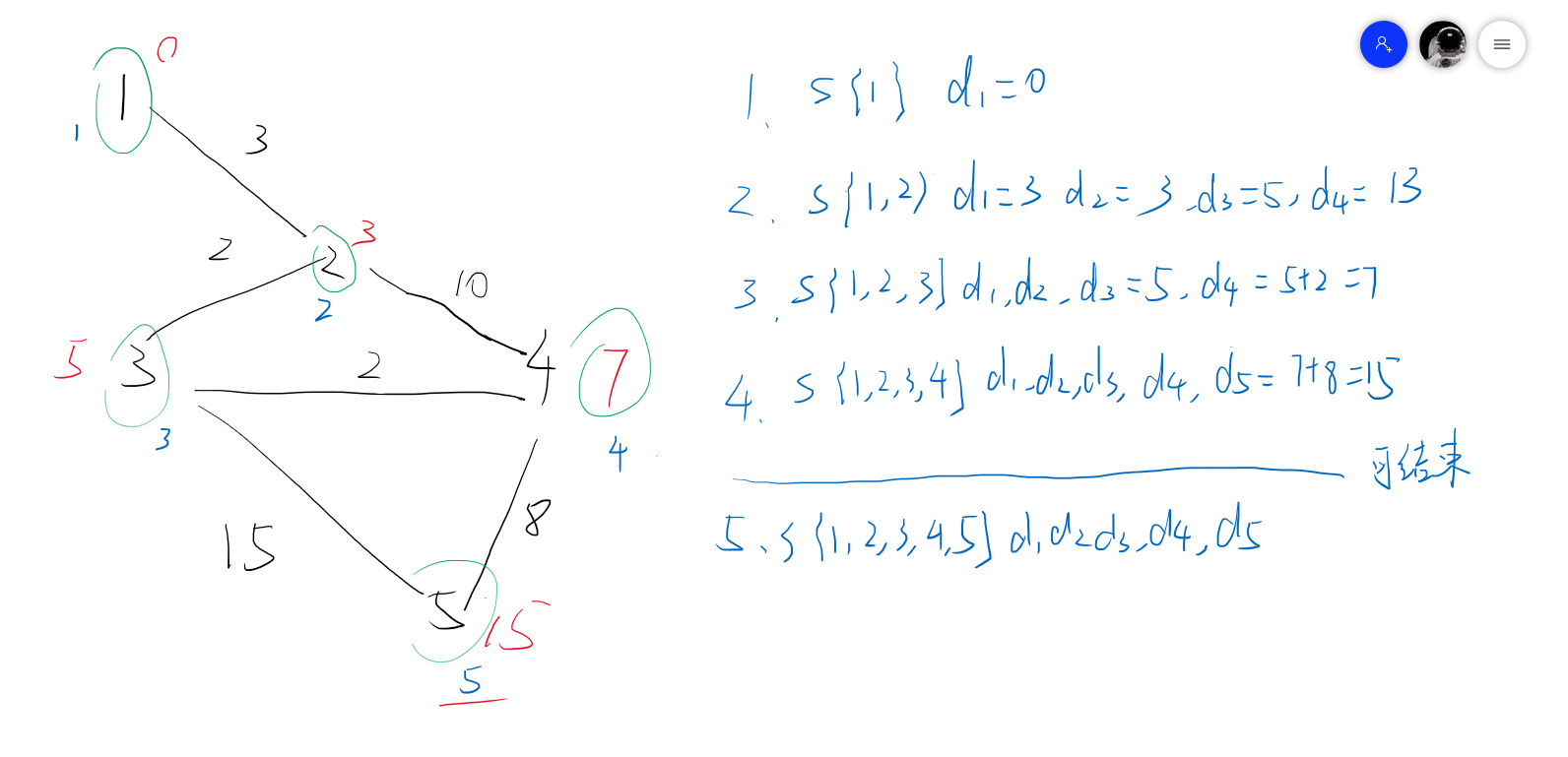
C++ 代码

/*
 * @Author: ACCXavier
 * @Date: 2021-04-21 17:50:23
 * @LastEditTime: 2021-04-22 12:22:52
 * Bilibili:https://space.bilibili.com/7469540
 * 题目地址:
 * @keywords: 
 */
#include <iostream>
#include <cstring>
using namespace std;
int n,m;
const int N  =510;
int g[N][N];//g[a][b]表示a点到b点的距离(a到b由一条边连接)
int dist[N];//dist[i]表示第一个点到第i个点的最短距离
bool st[N];
//编号a到b的最短距离,初始化的时候改为dist[a] = 0 ，以及return dist[b] 
int dijkstra()
{
    memset(dist,0x3f,sizeof dist);
    dist[1] = 0;
    for(int i = 0; i < n ;++ i){
        int t = -1;t

        //找未加入s集合中(st[j]==false)到1点最短的点
        for(int j = 1; j <= n; ++ j){
            if(!st[j]&&(t==-1||dist[t]>dist[j]))
                t = j;
        }
        if(t == n)break;//一个小优化 不需要用最后一点更新距离
        st[t] = true;//加入s集合
        for(int j = 1; j <= n; ++ j){
            if(!st[j]){//这个判断可以不要,因为先确定最短距离的点的距离已经比后确定的要小
                dist[j] = min(dist[j],dist[t]+g[t][j]);//用1~t+t~j更新1~j
            }
        }

    }
    if(dist[n]==0x3f3f3f3f)return -1;//别忘了判定
    return dist[n];

}

int main()
{
    memset(g,0x3f,sizeof g);
    cin>>n>>m;
    while(m--){
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        g[x][y] = min(g[x][y],z);//重边取最小
    }

    int ans = dijkstra();
    cout<<ans<<endl;
    return 0;
}

堆优化Dij $\mathrm{O}\left(\mathrm{n}\log\mathrm{m} \right) $

Dij算法最慢的一步是找不在S集合中距离起点最近的点t(找最小值),这一步是$\mathrm{O}(\mathrm{n})$的,用堆优化找最小值优化为$\mathrm{O}\left( \log\mathrm{n} \right) $

/*
 * @Author: ACCXavier
 * @Date: 2021-04-16 18:43:55
 * @LastEditTime: 2021-04-22 12:43:35
 * Bilibili:https://space.bilibili.com/7469540
 * 题目地址: https://www.acwing.com/problem/content/852/
 * @keywords: dijkstra2
 */
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
typedef pair<int ,int > PII;
const int N = 150010;//范围注意
int n,m;
int h[N],e[N],ne[N],idx,w[N];
int dist[N];
bool st[N];
void add(int a,int b,int c){
    e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx ++;
}
int dijkstra()
{

    memset(dist,0x3f,sizeof dist);

    dist[1] = 0;
    priority_queue<PII,vector<PII>,greater<PII> > q;//小根堆,{i,j}表示起点到j点距离为i
    //堆按第一个键排序,由于每次都要取距离最小的所以把距离放first
    q.push({0,1});//first是距离,second是点的编号


    while(q.size()){
        auto t = q.top();//取队头,最短
        q.pop();
        int ver = t.second,distance = t.first;
        if(st[ver]) continue;//如果这个点已经加入s集合 不用在更新

        st[ver] = true;//加入s集合

        for(int i = h[ver]; i != -1;i = ne[i]){//取这个点连接的所有点
            int j = e[i];
            if(dist[j]>dist[ver]+w[i]){//如果到j点距离大于 该点距离+该点到j点距离
                dist[j] = w[i] + dist[ver];//更新
                //dist[j] = w[i] + distance ;
                q.push({dist[j],j});//把这个距离入堆
            }
        }
    }
    if(dist[n]==0x3f3f3f3f)return -1;
    return dist[n];
}

int main()
{
    memset(h,-1,sizeof h);//!放在开头 不然插边不对
    scanf("%d%d",&n,&m);
    while(m--){
        int a, b ,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);

    }
    int d = dijkstra();
    cout<<d<<endl;
    return 0;
}