分析

答案和两个端点有关，考虑区间dp
dp[l][r] := str[l->r]上所有回文串集合的长度属性的最大值{闫氏dp}

考虑边界，当两端不同，去掉其中一个即 dp[l+1][r]/dp[l][r-1]
当两端相同，即 dp[l+1][r-1]+2
三者中取最大。

答案即原始长度减去1->L最大回文串的长度，考虑回文串的对称性，删除这几个等价于加上这几个。

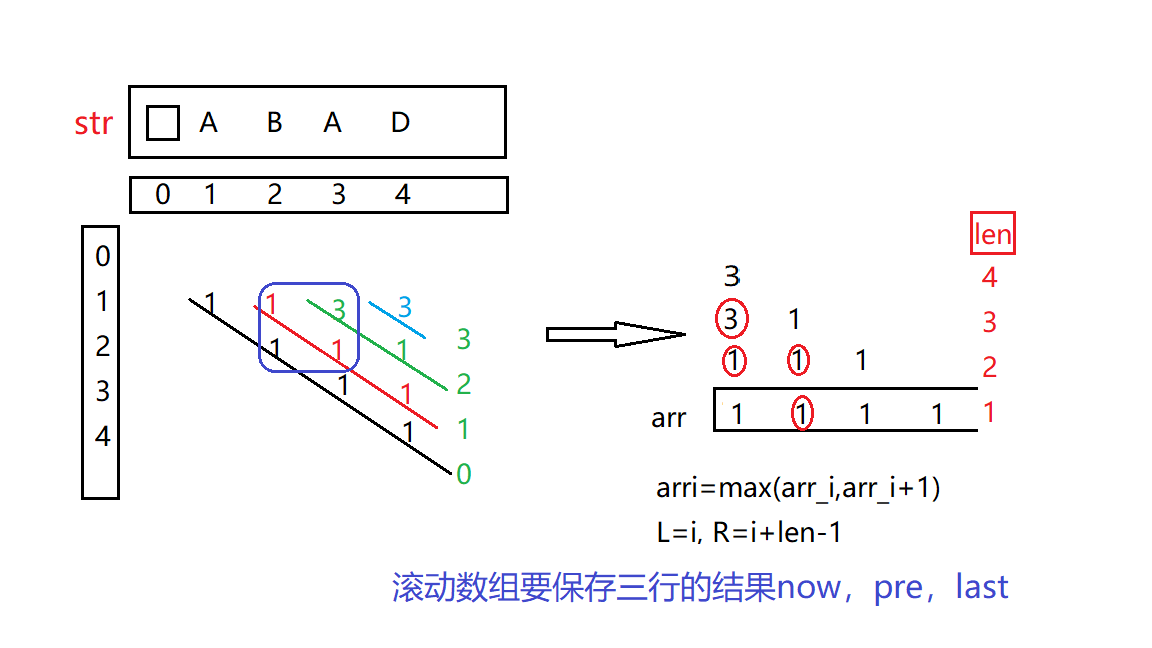
注意到每次都从右上到左下，要确定的是正方形框的右上角，他最多和另外三个值有关。如上图红色圈圈，考虑滚动数组用三行。

注意：考试不建议用滚动数组，需要考虑的细节比直接二维dp要多。

区间DP标准版

#include<iostream>
#include<algorithm>
#include<cstring>

#define ffor(i,s,e) for(int i=s;i<e;i++)
using namespace std;

char gs[1010];
int f[1010][1010];

int main(){
    scanf("%s",gs+1);
    int L=strlen(gs+1);

    ffor(i,0,L+1) f[i][i]=1;

    ffor(len,2,L+1){//枚举长度
        int maxLeft=L-len+1;
        ffor(left,1,maxLeft+1){//枚举左端点
            int right=left+len-1;
            f[left][right]=max(f[left+1][right],f[left][right-1]);
            if(gs[left]==gs[right])
                f[left][right]=max(f[left+1][right-1]+2,f[left][right]);
        }
    }

    cout<<L-f[1][L]<<endl;
    return 0;

}

滚动数组

#include<iostream>
#include<algorithm>
#include<cstring>

#define ffor(i,s,e) for(int i=s;i<e;i++)

using namespace std;

char gs[1010];
int f[3][1010];

int main(){
    scanf("%s",gs+1);  
    int L=strlen(gs+1);

    //初始化 前两行
    ffor(i,0,L+1) f[0][i]=1;
    ffor(i,0,L){
        f[1][i]=max(f[0][i],f[0][i+1]);
        if(gs[i]==gs[i+1]) f[1][i]=2;
    } 

    int now=2,pre=1,last=0;
    ffor(len,3,L+1){
        int iM=L-len+1;//当前行的最大位置
        ffor(i,1,iM+1){//如图中红色圆圈所示
            f[now][i]=max(f[pre][i],f[pre][i+1]);
            if(gs[i]==gs[i+len-1]) f[now][i]=max(f[now][i],f[last][i+1]+2);
        }
        //滚动
        swap(now,pre);
        swap(last,now);
    }

    cout<<L-f[pre][1]<<endl;
    return 0;

}