分析

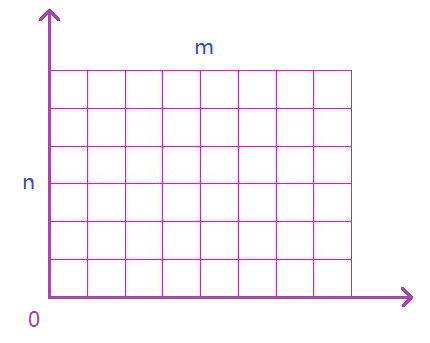
• 对于一个$n \times m$的网格，其格点的是$(n+1) \times (m+1)$的，这里为了处理方便，读入n、m后，直接都进行加一操作，变为格点数量，因此下面的分析中n、m表示的是格点的数量。

• 这里直接求解有多少种方案很难，因此我们需要曲线救国，先求出所有方案数，然后减去不合法的方案数，就可以得到最终的结果。

• 所有的方案数：$C_{n \times m}^3$。

• 不合法的方案数，所有不合法的方案必定是三点在同一条直线上，如果放在坐标系中来看，左下点为源点，则分为如下几种情况：

（1）斜率为0：$n \times C_m^3$；

（2）斜率为无穷大：$m \times C_n^3$；

（3）斜率大于0：首先这三个点在同一条线段上，假设该线段向x轴投影的长度为i，向y轴投影的长度为j，则所有的情况是(i, j)取遍(2,2)~(n,m)，如下图：

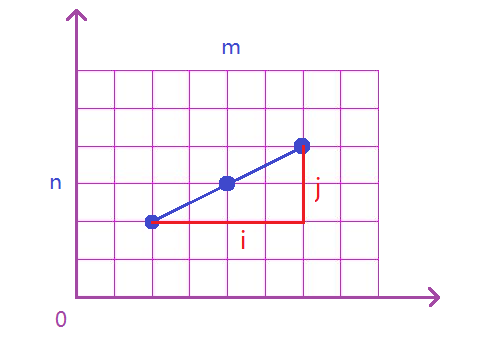
那么在这个会有多少这样的线段呢？我们只需要关注线段左端点有多少种取法即可，可以发现对于(i, j)，一共存在$(m - i) \times (n - j)$种取法；

然后还需要考虑一个问题，这个线段中中间的第三个点有多少中取法，也就是说这条线段会经过多少格点？如果不包括两个端点的话，答案是gcd(i, j)-1。关于这个问题的解释如下：

因此：所有斜率大于0的不合法方案为：
$$ \sum _{i, j} (m - i) \times (n - j) \times (gcd(i, j) - 1) \quad \quad 2 \le i \le n, 2 \le j \le m $$
（4）斜率小于0：和（3）是对称的，因此和（3）的方案数相同。

• 因此，最终合法的方案数为（其中$2 \le i \le n, 2 \le j \le m$）：

$$ C_{n \times m}^3 - n \times C_m^3 - m \times C_n^3 - 2 \times \sum _{i, j} (m - i) \times (n - j) \times (gcd(i, j) - 1) $$

• 结果不会超过$10^{18}$，因此可以使用long long存储结果。

代码

#include <iostream>

using namespace std;

typedef long long LL;

// 返回C(n, 3)
LL C(int n) {
    return (LL)n * (n - 1) * (n - 2) / 6;
}

int gcd(int a, int b) {
    return b ? gcd(b, a % b) : a;
}

int main() {

    int n, m;
    cin >> m >> n;

    n++, m++;

    LL res = C(n * m) - (LL)n * C(m) - (LL)m * C(n);
    for (int i = 2; i <= m; i++)  // m - i
        for (int j = 2; j <= n; j++)  // n - j
            res -= 2ll * (m - i) * (n - j) * (gcd(i, j) - 1);

    cout << res << endl;

    return 0;
}