分析

• 首先我们考虑如果是一个规则的图形，会有多少中放置方法：对于一个$n \times m$的长方形来说，需要放置k个车（车是无差别的），则对于行来说，我们可以从n行中选择k行来放置，即$C_n^k$；然后对于选择的k行，第一行可以有m种放置方法，第二行m-1种，根据乘法原理，对于选择的k行一共有$P_m^k$种选法。

• 因此对于一个一个$n \times m$的长方形来说，放置k个车的方案数是$C_n^k \times P_m^k$。

• 对于本题，我们可以将这个不规则的图形分成两个矩形，有两种分割方式，使用任意一种即可，这里将其分割为上下两个矩形，如下图：

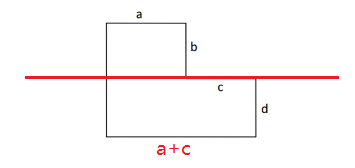
• 因为一共要放置k个车，我们可以枚举一下上下两个矩形中车的数量，假设上面矩形数量为i，则方案数为：

$$ \sum_{i=0}^k C_b^i \times P_a^i \times C_{d}^{k-i} \times P_{a+c-i}^{k-i} $$

• 这里求组合数的方式类似于AcWing 886. 求组合数 II，可以参考组合数的分析。

• 因为p=100003是一个质数，所以任何小于p的数都与p互质，因此逆元存在，另外由于p是质数，可以使用快速幂求解逆元。

代码

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 2010, mod = 100003;

int fact[N];  // 阶乘
int infact[N];  // 对应阶乘的逆元

// 快速幂
int qmi(int a, int k) {

    int res = 1 % mod;
    while (k) {
        if (k & 1) res = (LL)res * a % mod;
        a = (LL)a * a % mod;
        k >>= 1;
    }
    return res;
}

// 返回组合数
int C(int a, int b) {
    if (a < b) return 0;
    return (LL)fact[a] * infact[a - b] * infact[b] % mod;
}

// 返回排列数
int P(int a, int b) {
    if (a < b) return 0;
    return (LL)fact[a] * infact[a - b] % mod;
}

int main() {

    fact[0] = infact[0] = 1;
    for (int i = 1; i < N; i++) {
        fact[i] = (LL)fact[i - 1] * i % mod;
        infact[i] = (LL)infact[i - 1] * qmi(i, mod -2) % mod;
    }

    int a, b, c, d, k;
    cin >> a >> b >> c >> d >> k;

    int res = 0;
    for (int i = 0; i <= k; i++)
        res = (res + (LL)C(b, i) * P(a, i) % mod * C(d, k - i) % mod * P(a + c - i, k - i)) % mod;

    cout << res << endl;

    return 0;
}