分析

• 令牡牛为1，牝牛0，则问题是：任意两个1之间至少有K个0。

• 这一题使用到的技巧是递推，类似于DP中的状态转移（N头牛的位置下标为1~N）。

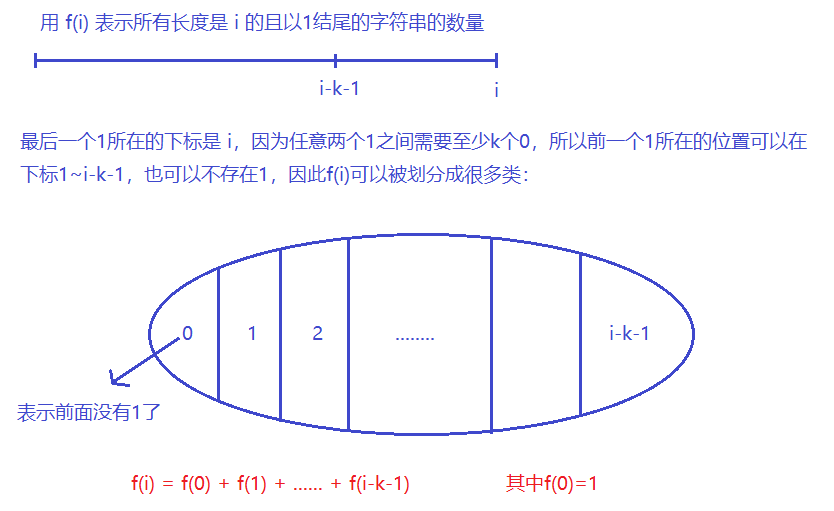
• 另外还需要考虑一些边界情况，即当i-k-1<0时，此时f(i) = f(0)。

• 此时我们还没求出所有的合法方案，因为f(n)表示最后一个1在第n个位置的方案数。所有的合法方案可以分为若干类，分类标准是最后一个1所在的位置，则没有1对应f(0)，最后一个1在第一个位置对应f(1)，......，因此将所有的f(i)加起来就是最后的结果。

• 求数组f可以使用前缀和求解。

代码

#include <iostream>

using namespace std;

const int N = 1000010, mod = 5000011;

int n, k;
int f[N];  // 长度为i且以1结尾的字符串的数量
int s[N];  // f的前缀和

int main() {

    cin >> n >> k;

    f[0] = s[0] = 1;
    for (int i = 1; i <= n; i++) {
        f[i] = s[max(i - k - 1, 0)];
        s[i] = (s[i - 1] + f[i]) % mod;
    }

    cout << s[n] << endl;

    return 0;
}