题目描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。

要求不能创建任何新的结点，只能调整树中结点指针的指向。

注意：

需要返回双向链表最左侧的节点。
例如，输入下图中左边的二叉搜索树，则输出右边的排序双向链表。

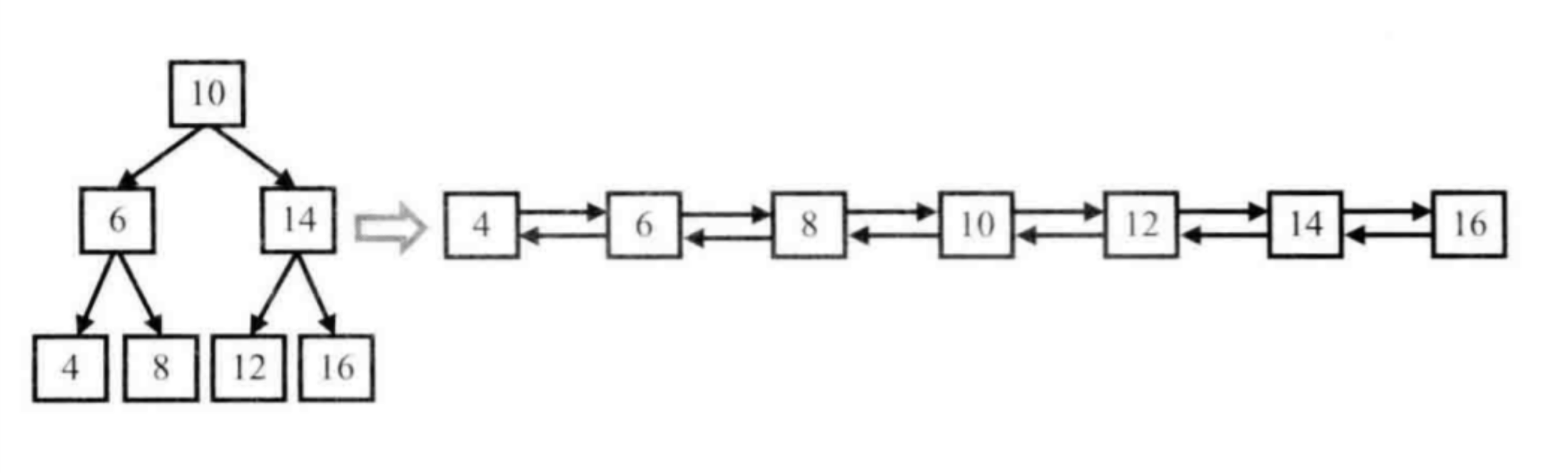
算法1

(暴力枚举) $O(n^2)$

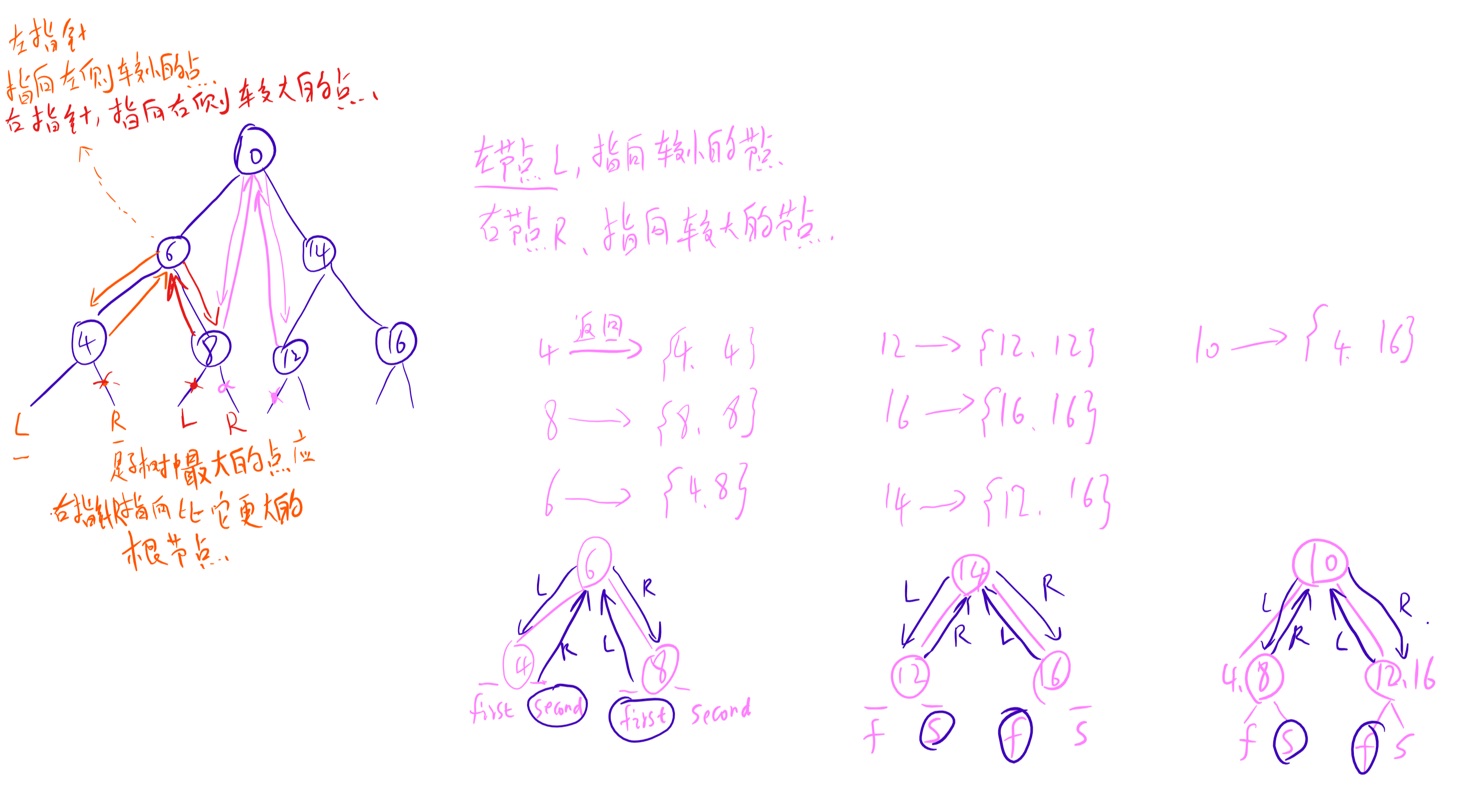
时间复杂度

参考文献

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* convert(TreeNode* root) {
        if(!root) return nullptr;
        auto res = dfs(root);
        return res.first;

    }
    pair<TreeNode*, TreeNode*> dfs(TreeNode *root){
        if(!root->left && !root->right) return {root, root};
        if(root->left && root->right){
            auto lside = dfs(root->left), rside = dfs(root->right);
            lside.second->right = root;
            root->left = lside.second;//左子树的最大值，和根节点拼接
            rside.first->left = root;
            root->right = rside.first;//右子树的最小值和根节点拼接
            return {lside.first, rside.second}; //返回整个子树的最小值，和最大值
        }
        if(root->left){
            auto lside = dfs(root->left);
            lside.second->right = root;
            root->left = lside.second;
            return {lside.first, root};
        }
        if(root->right){
            auto  rside = dfs(root->right);
            rside.first->left = root;
            root->right = rside.first;//右子树的最小值和根节点拼接
            return {root, rside.second}; //返回整个子树的最小值，和最大值
        }
    }

};