分析

• 假设满足条件的最小幸运数字如下：

$$ \underbrace{8......8}_{x个8} \quad \quad x \ge 1 $$

• 对这个数字进行变换，以方便分析处理：

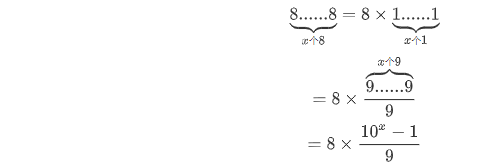
• 根据题目可知L能整除上述数据，所以有：

$$ L \ | \ 8 \times \frac{10 ^ x - 1}{9} $$

• 所以有：$9 \times L \ | \ 8 \times (10 ^ x - 1)$。

• 假设(L, 8) = d，因为9和8互质，所以：$(9 \times L, 8) = (L, 8) = d$。

• 所以有:

$$ \frac{9 \times L}{d} \ | \ \frac{8}{d} \times (10 ^ x - 1) $$

因为 $\frac{9 \times L}{d}$ 和 $\frac{8}{d}$ 互质，若令$C= \frac{9 \times L}{d}$，所以有：$C \ | \ (10 ^ x -1)$，即 $10 ^ x \equiv 1 \ (mod \ C)$。

• 根据 $10 ^ x \equiv 1 \ (mod \ C)$ 可知10必须和C互质，否则该式不可能成立，可以使用反证法证明，如果两者不互质，假设两者的最大公约数为d，则d>1，原式等价于 $m \times 10 ^ x + n \times C \equiv 1$，等式左边可以被d整除，等式右边却不可以，矛盾，无解，因此(10, C) == 1。

• 根据欧拉定理可知：$10 ^ {\phi(C)} \equiv 1 \ (mod \ C)$。因此 $\phi(C)$ 可以使得我们得到一个结果，但是这个结果并不一定是最小的，我们还要考虑如何求出最小的结果。

• 结论是：最小的一个$\phi(C)$的约数t就是最小的位数。证明如下（反证法）：

假设t是满足条件的最小的一个，则$10 ^ t \equiv 1 \ (mod\ C)$，且t不是$\phi(C)$的约数，则$\phi(C) = q \times t + r, 0 < r < t$，所以有$10^{\phi(C)} = 10 ^ {q \times t + r} \equiv 1 \ (mod\ C)$。

因为$10 ^ t \equiv 1 \ (mod\ C)$，所以 $10 ^ {qt} \equiv 1 \ (mod\ C)$，因此有$10 ^ r \equiv 1 \ (mod\ C)$，则我们找到一个更小的满足条件的数r，因此假设不成立。

• 因此，本题的步骤是：

（1）求L和8的最大公约数，记为d，然后求解$C= \frac{9 \times L}{d}$；

（2）根据公式求解$\phi(C)$，关于欧拉函数；

（3）枚举$\phi(C)$的约数，判断是否满足要求即可。

• 最后还有一点，快速幂中的乘法可能会超出long long的范围，因此乘法我们也要使用类似于快速幂的方式处理，称为龟速乘。对于$a \times b$，将b看成二进制进行相乘，假设$b=2^{x_1}+2^{x_2}+…2^{x_t}$，则：

$$ a \times b = a \times (2^{x_1}+2^{x_2}+…2^{x_t}) \\ = a \times 2 ^ {x_1} + a \times 2 ^ {x_2} + …+ a \times 2 ^ {x_t} $$

和快速幂十分类似，区别是将乘法换成加法即可（用复杂度换精度）。

• 当然，如果编译器支持__int128的话，也可以使用。

代码

#include <iostream>

using namespace std;

typedef long long LL;

// 返回C的欧拉函数值
LL get_euler(LL C) {

    LL res = C;
    for (LL i = 2; i <= C / i; i++)
        if (C % i == 0) {
            while (C % i ==0) C /= i;
            res = res / i * (i - 1);
        }
    if (C > 1) res = res / C * (C - 1);
    return res;
}

/*
// 龟速乘: (a * k) % p
LL qmul(LL a, LL k, LL p) {

    LL res = 0;
    while (k) {
        if (k & 1) res = (res + a) % p;
        a = (a + a) % p;
        k >>= 1;
    }
    return res;
}
// 快速幂: a ^ k % p
LL qmi(LL a, LL k, LL p) {

    LL res = 1 % p;
    while (k) {
        if (k & 1) res = qmul(res, a, p);
        a = qmul(a, a, p);
        k >>= 1;
    }
    return res;
}
*/

LL qmi(LL a, LL k, LL p) {

    LL res = 1 % p;
    while (k) {
        if (k & 1) res = (__int128)res * a % p;
        a = (__int128)a * a % p;
        k >>= 1;
    }
    return res;
}

int main() {

    int T = 1;
    LL L;
    while (cin >> L, L) {

        // (1) 求d, C
        int d = 1;
        while (L % (d * 2) == 0 && d * 2 <= 8) d *= 2;
        LL C = 9 * L / d;

        // (2) 求phi(C)
        LL phi = get_euler(C);

        // (3) 枚举phi(C)的约数，判断是否满足要求
        LL res = 1e18;
        if (C % 2 == 0 || C % 5 == 0) res = 0;  // 说明C和10不互质, 无解
        else {
            for (LL d = 1; d * d <= phi; d++)
                if (phi % d == 0) {
                    if (qmi(10, d, C) == 1) res = min(res, d);
                    if (qmi(10, phi / d, C) == 1) res = min(res, phi / d);
                }
        }
        printf("Case %d: %lld\n", T++, res);
    }

    return 0;
}