分析

• 分析如下：

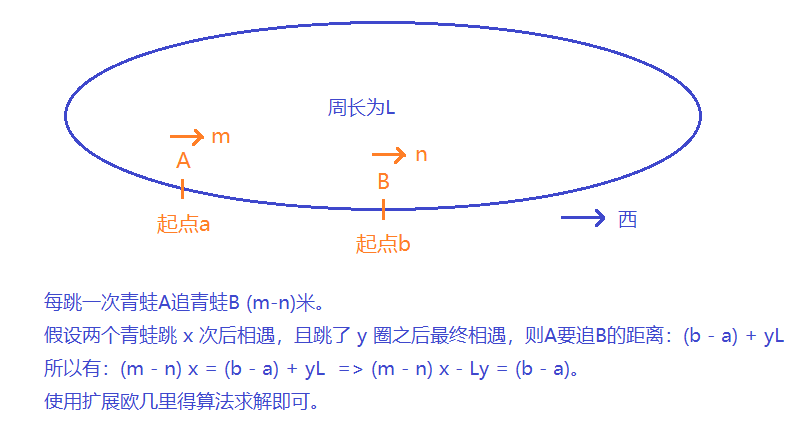
• 如果上述等式有解，则必须满足(m-n, L) | (b-a)，因为$(m-n) \times x + L \times y$一定是(m-n, L)的倍数，如果b-a不是(m-n, L)的倍数，则等式一定不可能成立。

• 如果满足(m-n, L) | (b-a)的话，由扩展欧几里得算法一定可以求出一组解。

• 最终求出的x还需要扩大$\frac{b - a}{(m-n, L)}$倍，因为裴蜀定理右侧为(m-n, L)，变成b需要左右同时扩大$\frac{b - a}{(m-n, L)}$倍。

• 假设我们得到一组解$x_0, y_0$，则所有解的通式如下（其中d=(m-n, L)）：

$$ \begin{cases} x = x_0 + \frac{L}{d} \times k \\\\ y = y_0 - \frac{m-n}{d}\times k \end{cases} \quad \quad k \in Z $$

则和AcWing 203. 同余方程类似，我们需要求出最小的正整数x，令$t = \frac{L}{d}$，则我们的结果为$(x_0 \% t + t) \% t$。

代码

#include <iostream>

using namespace std;

typedef long long LL;

LL exgcd(LL a, LL b, LL &x, LL &y) {

    if (!b) {
        x = 1, y = 0;
        return a;
    }

    LL d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

int main() {

    LL a, b, m, n, L;
    cin >> a >> b >> m >> n >> L;

    LL x, y;
    LL d = exgcd(m - n, L, x, y);
    if ((b - a) % d) puts("Impossible");
    else {
        x *= (b - a) / d;
        LL t = abs(L / d);
        cout << (x % t + t) % t << endl;
    }

    return 0;
}