题目
你有一架天平和 N 个砝码,这 N 个砝码重量依次是 W1, W2, · · · , WN。请你计算一共可以称出多少种不同的重量?
注意砝码可以放在天平两边。
算法
bitset
2021.5.4更新
首先bitset这个数据结构(蓝桥杯能看帮助文档的)
直接copy我打比赛的时候看的文档
C Bitsets
C Bitsets给程序员提供一种位集合的数据结构。Bitsets使用许多二元操作符,比如逻辑和,或等。
Constructors 创建新bitsets
Operators 比较和赋值bitsets
any() 如果有任何一个位被设置就返回true
count() 返回被设置的位的个数
flip() 反转bits中的位
none() 如果没有位被设置则返回true
reset() 清空所有位
set() 设置位
size() 返回可以容纳的位的个数
test() 返回指定位的状态
to_string() 返回bitset的字符串表示
to_ulong() 返回bitset的整数表示
一些解释
|能让状态不重- 先
<<再>>状态不漏 - 状态一定合法,
>>时不合法的状态都是<0(对应重物质量<0)的,bitset不记录负的。 <<|只放一边,>>|更新出重物边放砝码的所有状态>>|将一些砝码放在另一边,由于此时砝码边的所有状态都有了,在右边放一个g[i],不会出现大于g[i]的状态无法转移过来的,有人可能会认为由于g[i]不是有序的,这么干会让一些状态丢失,实则不会这样,因为所有状态的祖先都已经被更新出来,就类似<<时的s[0] = 1,顺序就无所谓了。
#include<iostream>
#include<bitset>
using namespace std;
const int N = 105, M = 100005;
int g[N], n;
bitset<M> S;
int main(){
scanf("%d", &n);
for(int i = 0; i < n; i ++ ){
scanf("%d", &g[i]);
}
S[0] = 1;
for(int i = 0; i < n; i ++ ){
S |= S << g[i];
}
for(int i = 0; i < n; i ++ ){
S |= S >> g[i];
}
cout << S.count() - 1 << endl;
return 0;
}


我看不懂,但我大受震撼
全部放左边
第一次循环表示,前
i个物品的权值只能为0,1的集合第二次循环,将右边等效到左边
第二次循环表示,前
i个物品的权值为0,1,-1,其他权值可以为0,1的集合具体思路,和解析请看如下图片。


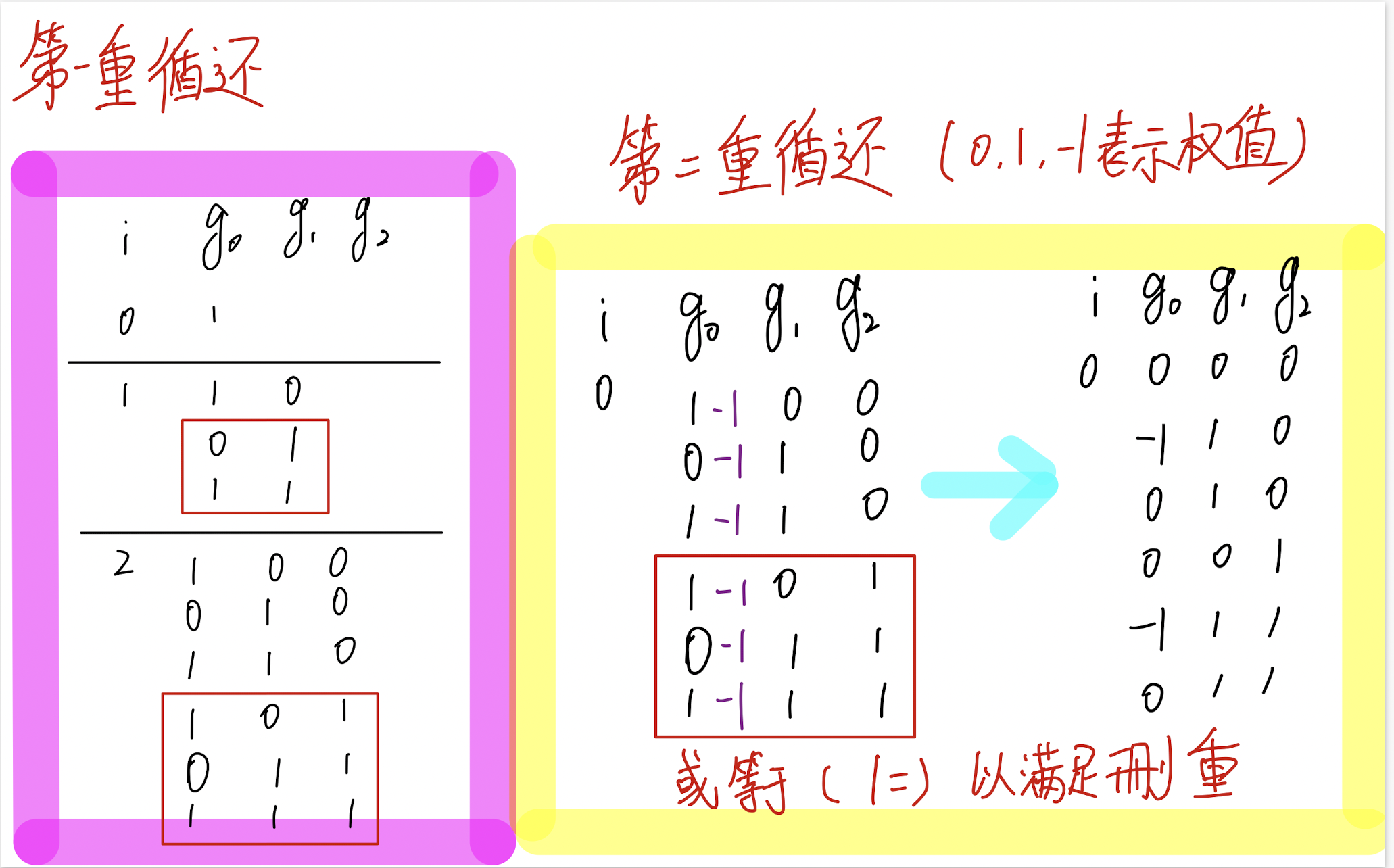
我看不懂,但我大受震撼
hh
题解
https://www.acwing.com/solution/content/167393/
自己的一些理解:
https://www.acwing.com/solution/content/237772/
我天,太妙了
https://www.bilibili.com/video/BV1rQ4y197L2/?spm_id_from=333.337.search-card.all.click
不懂的可以看看这个
学长yyds
orz
还能这么玩!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
我看不懂,但我大受震撼
我看不懂,但我大受震撼
我看不懂,但我大受震撼
我看不懂,但我大受震撼
我看不懂,但我大受震撼
我看不懂,但我大受震撼
nb
又是一个和我一样擅长计算机组成原理的同学
大佬能解释一下吗?我看不懂,但大受震撼
妙啊
大佬为什么向左移位再异或等价于往天平左边放砝码啊
下标表示重量,越往左越大,哪个位置为1就表示这个重量可以称取。左移gi后让所有的1移动到了原来位置加上gi的位置,相当于同一侧加砝码(第0位一开始设置成1,左移gi后gi位置为1),再异或上没移位前的状态就是此时的状态。