分析

• 如果$(x, y) = p$，且p是质数，则$(\frac{x}{p}, \frac{y}{p})=1$，说明$\frac{x}{p}, \frac{y}{p}$互质，令$a =\frac{x}{p}, b = \frac{y}{p}$，则相当于问在$1 \le a, b \le \frac{n}{p}$的条件下，互质的点对个数。和AcWing 201. 可见的点求解的内容很类似。

• 对于1~n中所有的质数，都需要求互质点对的个数，下面考虑对于某一个质数p，如何求解，如下图：

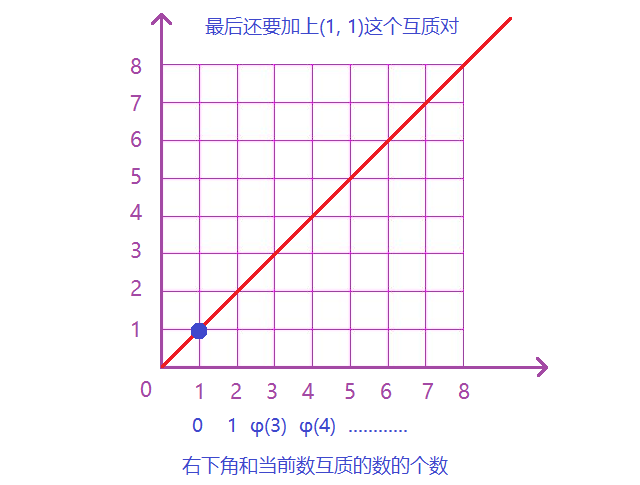
• 因此如果令$\phi(1)=0$，则对于对于当前考察的质数p，符合要求的点对数目为：$2 \times (\phi(1) + \phi(2) + … + \phi(\frac{n}{p}) + 1$。

• 我们需要对于1~n中所有的质数计算上述表达式，最后相加，因此可以采用前缀和思想求解。

分析

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 1e7 + 10;

// 1e7的int和bool数组大小都为40MB，LL数组大小80MB，因此使用存储空间为200MB
int primes[N], cnt;
bool st[N];
int phi[N];
LL s[N];

void init(int n) {

    // 默认phi[1] == 0
    for (int i = 2; i <= n; i++) {
        if (!st[i]) {
            primes[cnt++] = i;
            phi[i] = i - 1;
        }
        for (int j = 0; primes[j] * i <= n; j++) {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) {
                phi[primes[j] * i] = phi[i] * primes[j];
                break;
            }
            phi[primes[j] * i] = phi[i] * (primes[j] - 1);
        }
    }

    for (int i = 1; i <= n; i++) s[i] = s[i - 1] + phi[i];
}

int main() {

    int n;
    cin >> n;

    init(n);

    LL res = 0;
    for (int i = 0; i < cnt; i++) {
        int p = primes[i];
        res += s[n / p] * 2 + 1;
    }

    cout << res << endl;

    return 0;
}