分析

• 首先是结论：点$(x_0, y_0)$是可见的 $\iff$ $x_0, y_0$是互质的。下面证明这个结论。

• 首先是充分性：反证法，如果$(x_0, y_0)$不是互质的，设其最大公约数为d，则d > 1，因此$(\frac{x_0}{d}, \frac{y_0}{d})$会把$(x_0, y_0)$遮住（因为斜率相同），充分性成立。

• 必要性：反证法，如果$(x_0, y_0)$是互质的，但是不可见，则说明一定存在$x < x_0, y < y_0$使得$\frac{y_0}{x_0} == \frac{y}{x}$，说明可以被约分，则推出$(x_0, y_0)$不是互质的，矛盾，必要性成立。

• 因此本题中相当于让我们求解对于$0 \le x, y \le N$，有多少数对$(x, y)$是互质的。我们可以先考虑一般的情况，如下图的右下部分：

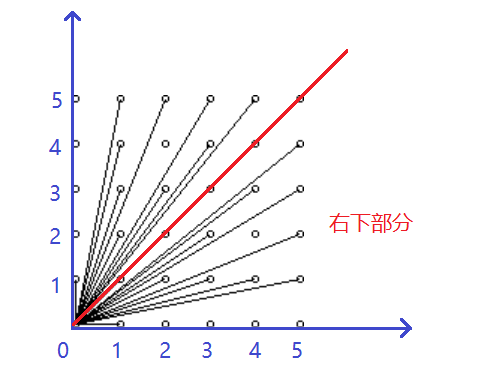
只考虑右下部分，则和1互质的点为$\phi(1) = 1$个，和2互质的点有$\phi(2) = 1$个，......，和n互质的点有$\phi(n)$个。

• 因为对称性，上半部分的数量等于下半部分的数量，答案为

$$ \sum _ {i = 1} ^ n \phi(i) + 1 $$

代码

#include <iostream>

using namespace std;

const int N = 1010;

int primes[N], cnt;
bool st[N];
int phi[N];

// 筛法求欧拉函数
void init(int n) {

    phi[1] = 1;
    for (int i = 2; i <= n; i++) {
        if (!st[i]) {
            primes[cnt++] = i;
            phi[i] = i - 1;
        }
        for (int j = 0; primes[j] * i <= n; j++) {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) {
                phi[i * primes[j]] = phi[i] * primes[j];
                break;
            }
            phi[i * primes[j]] = phi[i] * (primes[j] - 1);
        }
    }
}

int main() {

    init(N - 1);

    int n, m;
    cin >> m;
    for (int T = 1; T <= m; T++) {
        cin >> n;
        int res = 1;
        for (int i = 1; i <= n; i++) res += phi[i] * 2;
        cout << T << ' ' << n << ' ' << res << endl;
    }

    return 0;
}