分析

• 我们需要对式子进行化简，原始表达式如下：

$$ \frac{1}{x} + \frac{1}{y} = \frac{1}{n!} $$

通分并十字相乘得到：
$$ (x + y) \times n! = x \times y $$
继续化简，我们可以得到y的表达式：
$$ y = \frac{x \times n!}{x - n!} = \frac{(x-n!+n!) \times n!}{x - n!} = n! + \frac{(n!) ^ 2}{x - n!} $$
因为题目要求x、y都是正整数，又$\frac{1}{y} = \frac{1}{n!} - \frac{1}{x}$，所以$x > n!$，即$x - n! > 0$。

• 因为y是正整数，所以 $\frac{(n!) ^ 2}{x - n!}$ 必须是整数，又 $x - n! > 0$，所以相当于问 $(n!)^2$ 有多少约数。

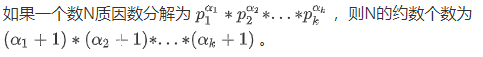
• 所以我们可以将 $n!$ 进行质因数分解（对应AcWing 197. 阶乘分解）

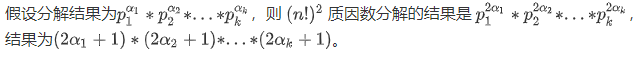
代码

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 1000010, mod = 1e9 + 7;

int primes[N], cnt;
bool st[N];

void init(int n) {

    for (int i = 2; i <= n; i++) {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] * i <= n; j++) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int main() {

    int n;
    cin >> n;

    init(n);

    int res = 1;
    for (int i = 0; i < cnt; i++) {
        int p = primes[i];
        int s = 0;
        for (int j = n; j; j /= p) s += j / p;
        res = (LL)res * (2 * s + 1) % mod;
    }

    printf("%d\n", res);

    return 0;
}