仔细读题发现，这题的操作其实就是next_permutation()的逆操作，一次操作相当于求当前序列的前一个排列。

• 因此这道题求的是当前这个序列是第几个排列,因此可以用康托展开(没学过)，也可以用数位DP(代码更简单)。。

在此之前需要解决几个数学知识：

1. 若干个字母求排列方案数：求$n_{1}$个$a$、$n_{2}$个$b$、$n_{3}$个$c$…的排列方案数，令$n=\sum_{i = 1}^{k}{n_i}$，则$ans=(n!)/\prod_{i = 1}^{k}{n_i}$

2. 逆元：因为涉及到取模和除法，因此不能之前进行除运算，应该转换为逆元，再进行乘法运算，因为这里取模的值是一个质数，因此可以直接利用费马定理，使用快速幂求逆元。

现在来看一个排列的次序是多少：
通过枚举的方式，若在原序列中当前位置是s[i]，那么当前这位可以枚举的字母有两种：
1.$a——s[i]-1$，此时因为枚举的字母都小于$s[i]$,因此后面的字母可以随意排列，结果是$(n!)/\prod_{i = 1}^{k}{n_i}$（高位的取值都小于原字母，后面不管怎么样都不会影响最终结果了）
2.$s[i]$：此时该位选择的字母与原序列的相同，因此需要继续向后处理即可。
其实就是找出小于当前这个序列的序列数

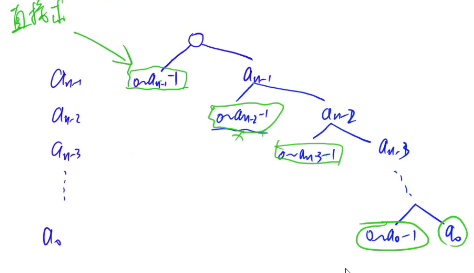
原理图如下：

typedef long long LL;
const int mod = 1e9 + 7;
const int N = 3010;

class Solution {
public:
    LL f[N] , inf[N];
    vector<int> cnt;

    LL qmi(LL a , int b)
    {
        LL res = 1;
        while(b)
        {
            if(b & 1) res = res * a % mod;
            a = a * a % mod;
            b >>= 1;
        }
        return res;
    }

    int get()//若干个字母求排列方案数
    {
        int sum = 0;
        for(int i = 0 ; i < 26 ; i++) sum += cnt[i];
        int res = f[sum];
        for(int i = 0 ; i < 26 ; i++)
            res = (LL)res * inf[cnt[i]] % mod;
        return res;
    }

    int makeStringSorted(string s) {
        cnt = vector<int>(26 , 0);

        f[0] = inf[0] = 1;
        for(int i = 1 ; i <= s.size() ; i++)//预处理阶乘数组和阶乘的逆元数组
        {
            f[i] = f[i - 1] * i % mod;
            inf[i] = inf[i - 1] * qmi(i , mod - 2) % mod;
        }

        for(auto c : s) cnt[c - 'a']++;//记录每个字母出现的次数

        int res = 0;
        for(auto c : s)
        {
            int x = c - 'a';
            for(int i = 0 ; i < x ; i++)//枚举a到s[i]-1
            {
                if(cnt[i] == 0) continue;
                cnt[i]--;
                res = (res + get()) % mod;
                cnt[i]++;
            }
            cnt[x]--;//当前这为设置为s[i]，因此在后面它出现的次数就少一次
        }
        return res;
    }
};