题目描述

给你一个数组 points，其中 points[i] = [x_i, y_i]，表示第 i 个点在二维平面上的坐标。多个点可能会有 相同 的坐标。

同时给你一个数组 queries，其中 queries[j] = [x_j, y_j, r_j]，表示一个圆心在 (x_j, y_j) 且半径为 r_j 的圆。

对于每一个查询 queries[j]，计算在第 j 个圆 内 点的数目。如果一个点在圆的 边界上，我们同样认为它在圆 内。

请你返回一个数组 answer，其中 answer[j] 是第 j 个查询的答案。

样例

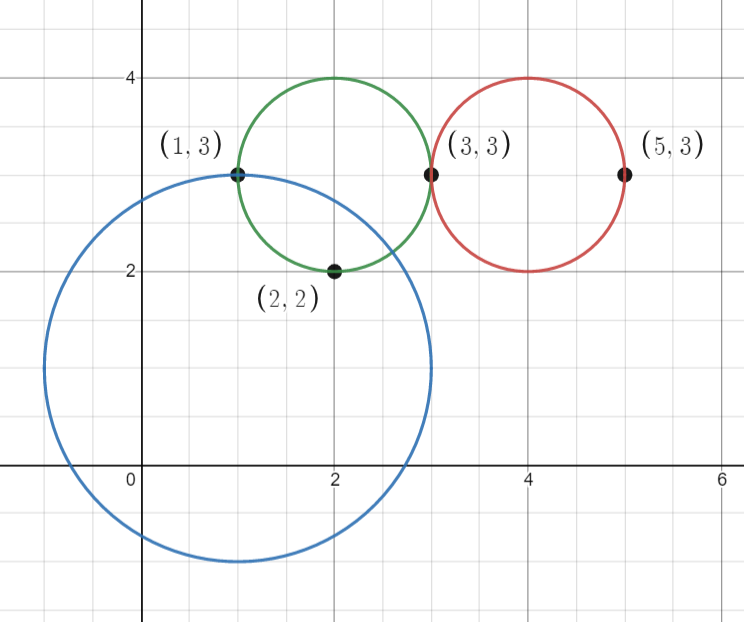
输入：points = [[1,3],[3,3],[5,3],[2,2]], queries = [[2,3,1],[4,3,1],[1,1,2]]
输出：[3,2,2]
解释：所有的点和圆如上图所示。
queries[0] 是绿色的圆，queries[1] 是红色的圆，queries[2] 是蓝色的圆。

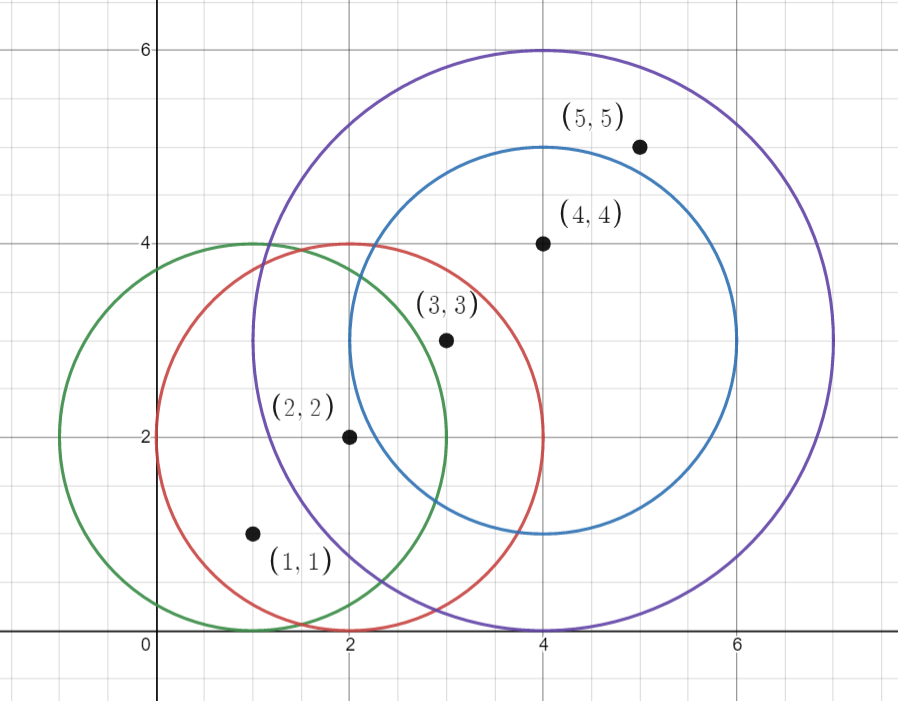
输入：points = [[1,1],[2,2],[3,3],[4,4],[5,5]], queries = [[1,2,2],[2,2,2],[4,3,2],[4,3,3]]
输出：[2,3,2,4]
解释：所有的点和圆如上图所示。
queries[0] 是绿色的圆，queries[1] 是红色的圆，queries[2] 是蓝色的圆，queries[3] 是紫色的圆。

限制

• 1 <= points.length <= 500
• points[i].length == 2
• 0 <= x_i, y_i <= 500
• 1 <= queries.length <= 500
• queries[j].length == 3
• 0 <= x_j, y_j <= 500
• 1 <= r_j <= 500
• 所有的坐标都是整数。

算法

(暴力枚举) $O(nq)$

1. 对于每个询问，暴力枚举所有的点，判断是否在圆内。

时间复杂度

• 对于每个询问，需要 $O(n)$ 的时间计算答案，故总时间复杂度为 $O(nq)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储答案。

C++ 代码

class Solution {
public:
    vector<int> countPoints(vector<vector<int>>& points, vector<vector<int>>& queries) {
        vector<int> ans;
        for (const auto &q : queries) {
            int x = q[0], y = q[1], r = q[2];
            int tot = 0;

            for (const auto &p : points) {
                int x0 = p[0], y0 = p[1];
                if ((x - x0) * (x - x0) + (y - y0) * (y - y0) <= r * r)
                    tot++;
            }
            ans.push_back(tot);
        }

        return ans;
    }
};