分析

• 因为整个集合的最大值是不断减小的，因此游戏一定可以停止。

• 这一题类似于AcWing 893. 集合-Nim游戏，我们仍然可以将每堆石子看成一个有向图，我们计算出每个图初始的SG，将所有这些值异或起来即可，如果不等于0，先手必胜，否则先手必败。

• 问题在于每次一堆石子可能变成两堆，如下图：

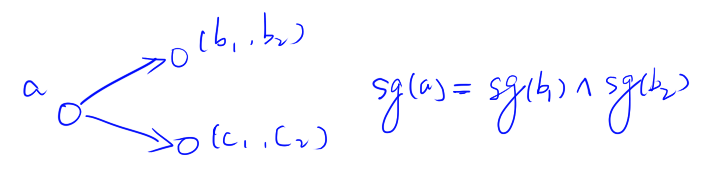
我们只需要使用 $sg(a)=sg(b_1) \oplus sg(b_2)$ 计算即可。

代码

#include <iostream>
#include <cstring>
#include <unordered_set>

using namespace std;

const int N = 110;

int n;
int f[N];  // 记忆化搜索, 记录每个节点对应的sg值

int sg(int x) {

    if (f[x] != -1) return f[x];

    unordered_set<int> S;
    for (int i = 0; i < x; i++)
        for (int j = 0; j <= i; j++)
            S.insert(sg(i) ^ sg(j));

    for (int i = 0; ; i++)
        if (!S.count(i))
            return f[x] = i;
}

int main() {

    cin >> n;

    memset(f, -1, sizeof f);

    int res = 0;
    for (int i = 0; i < n; i++) {
        int x;
        cin >> x;
        res ^= sg(x);
    }

    if (res) puts("Yes");
    else puts("No");

    return 0;
}