题目描述

小蓝要用七段码数码管来表示一种特殊的文字。

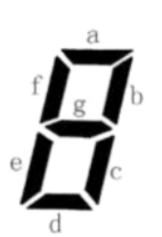
上图给出了七段码数码管的一个图示，数码管中一共有 7 段可以发光的二 极管，分别标记为 a, b, c, d, e, f, g。
小蓝要选择一部分二极管（至少要有一个）发光来表达字符。在设计字符 的表达时，要求所有发光的二极管是连成一片的。
例如： b 发光，其他二极管不发光可以用来表达一种字符。
例如： c 发光，其他二极管不发光可以用来表达一种字符。这种 方案与上 一行的方案可以用来表示不同的字符，尽管看上去比较相似。
例如： a, b, c, d, e 发光， f, g 不发光可以用来表达一种字符。
例如： b, f 发光，其他二极管不发光则不能用来表达一种字符，因为发光 的二极管没有连成一片。
请问，小蓝可以用七段码数码管表达多少种不同的字符？

DFS+并查集

中间有一个出错的地方在于，我是把边转换成点之后改成了图，然后使用邻接矩阵进行存储，但是在转换成图的时候，少加了两条边（图片中两条红边），导致最后算出来的结果要少于答案。

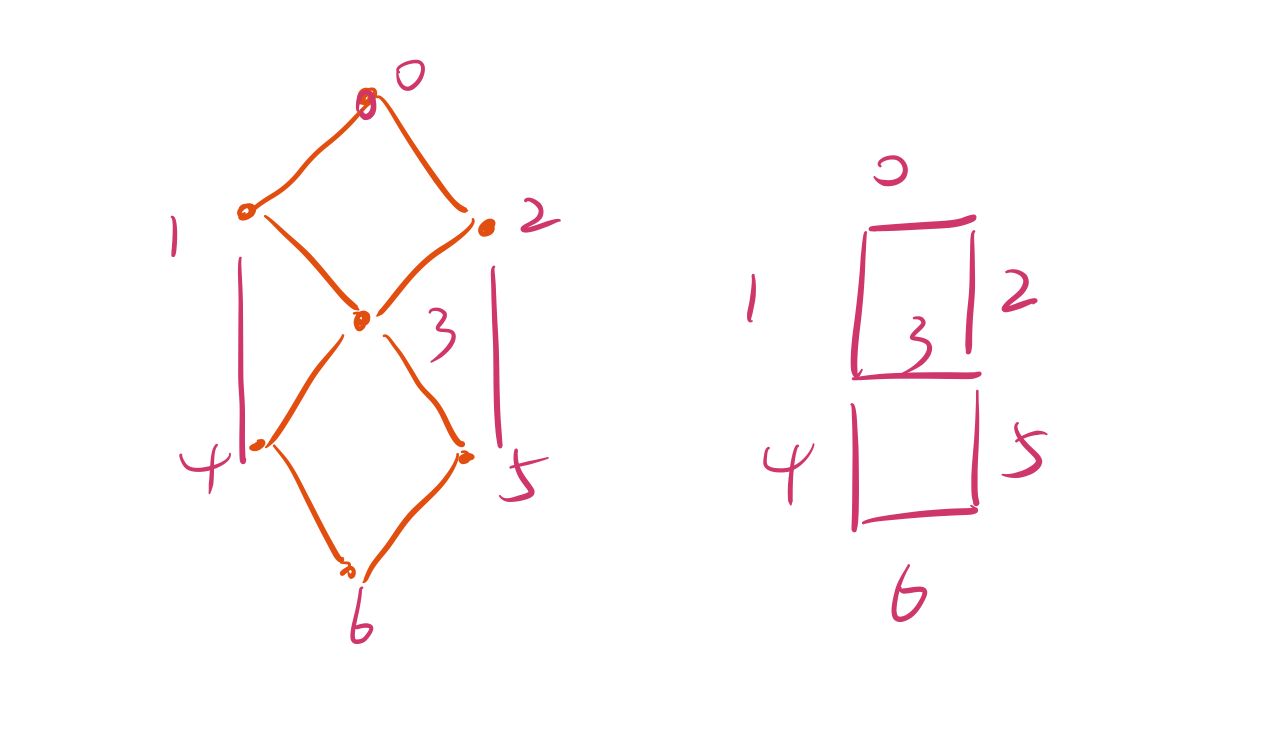
发现这个错误是在过程中把每一种生成的情况都输出，对照看了一下发现有少的情况。

解题步骤：
1.首先是使用DFS搜每一种情况

void dfs(int u){
    //结束时情况

    //遍历每一种情况
        //判断不合法情况

        //合法情况，走向下一步，进行标记
        //dfs(u+1)
        //回溯（回复现场）

}
对于每一个灯来说，有灭（0）和亮（1）两种情况
所以遍历每一种情况进行DFS就是：当前灯亮之后下一个灯，和当前灯灭之后下一个灯
结束情况就是灯已经到最后一个了（>=7）

2.由于DFS是一条路走到黑，所以每次到结束情况时，数组中存储的是当前这一种情况的灯的暗灭情况，也就是说我们可以在DFS结束情况中进行连通的判断
3.连通判断使用的是并查集，对于当前情况中每一个亮的灯，遍历它的边集，如果它的连通边中有当前情况也亮着的灯，就把他们两个合并，最后如果当前亮着的灯在同一个集合中，就说明这一种情况是连通的。
4.每一次判断完是否连通要返回的时候，记得要恢复现场（并查集父集合初始化），便于下次判断使用。

C++ 代码

#include<iostream>

using namespace std;
int mp[10],res,g[10][10],fa[100];
int find(int a){
    if(fa[a]!=a) fa[a]=find(fa[a]);
    return fa[a];
}

void merge(int a,int b){
    fa[find(a)]=find(b);
}

void init(){
    for(int i=0;i<100;i++){
        fa[i]=i;
    }
}

void dfs(int n){
    if(n>=7){

        for(int i=0;i<7;i++){
            if(mp[i]==1){
                for(int j=0;j<7;j++){
                    if(g[i][j]==1&&mp[j]==1) merge(i,j);
                }
            }
        }

        int t=-1,m=0;
        for(;m<7;m++){
            if(mp[m]==1&&t==-1) t=find(m);
            if(mp[m]==1&&find(m)!=t) break;
        }
        if(m==7&&t!=-1) res++; //注意全灭的情况

        init();
        return;
    }

    mp[n]=0;
    dfs(n+1);

    mp[n]=1;
    dfs(n+1);
}


int main(){
    for(int i=0;i<7;i++){
        g[i][i]=1;
    }
    g[0][1]=g[1][0]=g[0][2]=g[2][0]=1;
    g[1][3]=g[3][1]=g[1][4]=g[4][1]=1;
    g[2][3]=g[3][2]=g[2][5]=g[5][2]=1;
    g[3][4]=g[4][3]=g[3][5]=g[5][3]=1;
    g[4][6]=g[6][4]=1;
    g[5][6]=g[6][5]=1;

    init();
    dfs(0);
    cout<<res<<endl;

    return 0;
}