十大排序算法总结
概述
-
排序问题是算法领域一个十分重要的问题,如果一组数组是有序的,我们可以在此基础上解决很多问题。
-
对于排序问题,总的来说 内排序 和 外排序。
-
内排序:指待排序列完全存放在内存中所进行的排序过程,适合数据量不太大的元素序列。
-
外排序:指排序过程中还需访问外存储器,足够大的元素序列,因不能完全放入内存,只能使用外排序。
-
这里只介绍内排序。
-
另外还要明确一个概念:排序算法的稳定性。
若对任意的数据元素序列,使用某个排序方法,对它按关键字进行排序:若相同关键字元素间的位置关系,排序前与排序后保持一致,称此排序方法是稳定的;而不能保持一致的排序方法则称为不稳定的。比如两个关键字都为2,排序前和排序后这两个2的相对顺序没有发生改变,则该排序算法是稳定的。
- 排序算法概览
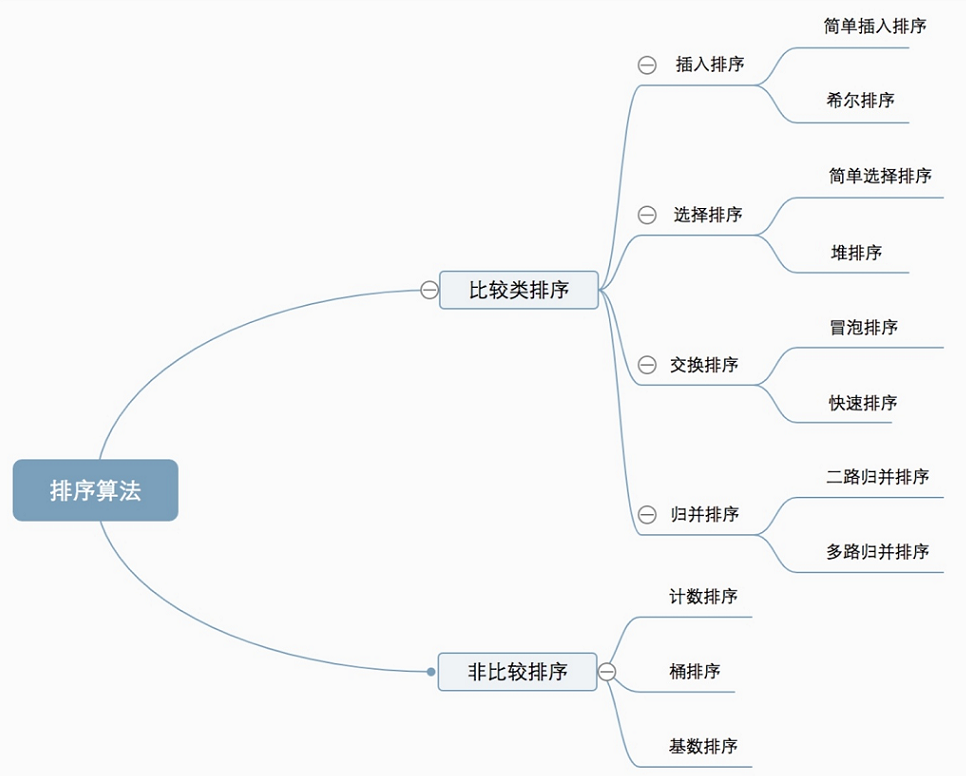
| 排序方法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 | 说明 |
|---|---|---|---|---|---|---|
| 简单插入排序 | $O(n^2)$ | $O(n^2)$ | $O(n)$ | $O(1)$ | 稳定 | |
| 希尔排序 | $O(n^{1.3})$ | $O(n^2)$ | $O(n)$ | $O(1)$ | 不稳定 | 2 2 1 |
| 简单选择排序 | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 不稳定 | 2 2 1 |
| 堆排序 | $O(nlog_2 n)$ | $O(nlog_2 n)$ | $O(nlog_2 n)$ | $O(1)$ | 不稳定 | 2 1 1 |
| 冒泡排序 | $O(n^2)$ | $O(n^2)$ | $O(n)$ | $O(1)$ | 稳定 | |
| 快速排序 | $O(nlog_2 n)$ | $O(n^2)$ | $O(nlog_2 n)$ | $O(n)$ | 不稳定 | 2 1 1 |
| 二路归并排序 | $O(nlog_2 n)$ | $O(nlog_2 n)$ | $O(nlog_2 n)$ | $O(n)$ | 稳定 | |
| 计数排序 | $O(n+k)$ | $O(n+k)$ | $O(n+k)$ | $O(n+k)$ | 稳定 | 数据范围0~k |
| 桶排序 | S | S | S | $O(n)$ | 稳定 | 桶个数为m |
| 基数排序 | $O(n*d)$ | $O(n*d)$ | $O(n*d)$ | $O(n)$ | 稳定 | 数据最长长度为d |
-
上表中 S代表:$O(n*log_2(n/m)+n)$ 。
-
可以直接复制代码到如下网站进行测试:AcWing,如下的各种排序算法代码都可以在这个测试测试。
问题描述:给出一组数据,请将这组数据升序排列。
一. 插入排序
1.1 简单插入排序
分析

代码
- C++
// Created by WXX on 2021/3/1 11:47
#include <iostream>
using namespace std;
const int N = 1010; // 输入数据个数的的上限
int n; // 实际元素个数
int q[N];
void sort() {
for (int i = 1; i < n; i++) {
int t = q[i], j = i;
for (; j > 0 && q[j - 1] > t; j--) q[j] = q[j - 1];
q[j] = t;
}
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &q[i]);
sort();
for (int i = 0; i < n; i++) printf("%d ", q[i]);
printf("");
return 0;
}
- Java
import java.util.Scanner;
/**
* Created by WXX on 2021/3/1 11:24
*/
public class Main {
public static final int N = 1010; // 输入数据个数的的上限
static int n; // 实际元素个数
static int[] q = new int[N];
private static void sort() {
for (int i = 1; i < n; i++) {
int t = q[i], j = i;
for (; j > 0 && q[j - 1] > t; j--) q[j] = q[j - 1];
q[j] = t;
}
}
public static void main(String[] args) {
Scanner sn = new Scanner(System.in);
n = sn.nextInt();
for (int i = 0; i < n; i++) q[i] = sn.nextInt();
sort();
for (int i = 0; i < n; i++) System.out.print(q[i] + " ");
System.out.println();
}
}
1.2 希尔排序
分析

代码
- C++
// Created by WXX on 2021/3/1 12:00
#include <iostream>
using namespace std;
const int N = 1010;
int n;
int q[N];
void shell_sort(int d) {
for (int i = d; i < n; i++) {
int t = q[i], j = i;
for (; j >= d && q[j - d] > t; j -= d) q[j] = q[j - d];
q[j] = t;
}
}
void sort() {
int d[] = {5, 3, 1};
for (int step : d) shell_sort(step);
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &q[i]);
sort();
for (int i = 0; i < n; i++) printf("%d ", q[i]);
printf("");
return 0;
}
- Java
import java.util.Scanner;
/**
* Created by WXX on 2021/3/1 11:50
*/
public class Main {
public static final int N = 1010;
static int n;
static int[] q = new int[N];
private static void shellSort(int d) {
for (int i = d; i < n; i++) {
int t = q[i], j = i;
for (; j >= d && q[j - d] > t; j -= d) q[j] = q[j - d];
q[j] = t;
}
}
private static void sort() {
int[] d = {5, 3, 1};
for (int step : d) shellSort(step);
}
public static void main(String[] args) {
Scanner sn = new Scanner(System.in);
n = sn.nextInt();
for (int i = 0; i < n; i++) q[i] = sn.nextInt();
sort();
for (int i = 0; i < n; i++) System.out.print(q[i] + " ");
System.out.println();
}
}
二. 选择排序
2.1 简单选择排序
分析
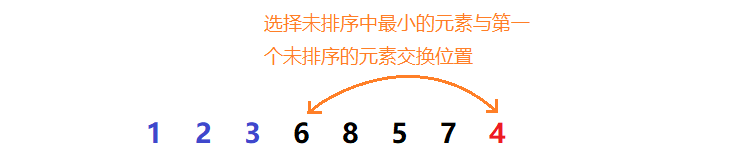
代码
- C++
// Created by WXX on 2021/3/1 14:28
#include <iostream>
using namespace std;
const int N = 1010;
int n;
int q[N];
void sort() {
for (int i = 0; i < n - 1; i++) {
int k = i; // 未排序的数据中最小值对应的下标
for (int j = i + 1; j < n; j++)
if (q[j] < q[k])
k = j;
swap(q[i], q[k]);
}
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &q[i]);
sort();
for (int i = 0; i < n; i++) printf("%d ", q[i]);
printf("");
return 0;
}
- Java
import java.util.Scanner;
/**
* Created by WXX on 2021/3/1 14:34
*/
public class Main {
public static final int N = 1010;
static int n;
static int[] q = new int[N];
private static void sort() {
for (int i = 0; i < n - 1; i++) {
int k = i; // 未排序的数据中最小值对应的下标
for (int j = i + 1; j < n; j++)
if (q[j] < q[k])
k = j;
int t = q[i]; q[i] = q[k]; q[k] = t; // 交换q[i]和q[k]的值
}
}
public static void main(String[] args) {
Scanner sn = new Scanner(System.in);
n = sn.nextInt();
for (int i = 0; i < n; i++) q[i] = sn.nextInt();
sort();
for (int i = 0; i < n; i++) System.out.print(q[i] + " ");
System.out.println();
}
}
2.2 堆排序
分析
- 首先用筛选法创建大顶堆,然后每次将堆顶元素换到最后再shiftDown,如此循环即可。
代码
- C++
// Created by WXX on 2021/3/1 14:59
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int q[N];
void down(int u) {
int k = u;
if (2 * u <= n && q[2 * u] > q[k]) k = 2 * u;
if (2 * u + 1 <= n && q[2 * u + 1] > q[k]) k = 2 * u + 1;
if (k != u) {
swap(q[k], q[u]);
down(k);
}
}
void sort() {
// 筛选法建堆,时间复杂度O(n),大根堆
for (int i = n / 2; i >= 1; i--) down(i);
int size = n;
while (n) {
swap(q[n], q[1]);
n--;
down(1);
}
n = size;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &q[i]);
sort();
for (int i = 1; i <= n; i++) printf("%d ", q[i]);
printf("");
return 0;
}
- Java
import java.io.BufferedReader;
import java.io.InputStreamReader;
/**
* Created by WXX on 2021/3/1 14:40
* 注意:为了方便这里存储数据从q1开始,q0未使用
*/
public class Main {
public static final int N = 100010;
static int n;
static int[] q = new int[N];
private static void down(int u) {
int k = u;
if (2 * u <= n && q[2 * u] > q[k]) k = 2 * u;
if (2 * u + 1 <= n && q[2 * u + 1] > q[k]) k = 2 * u + 1;
if (k != u) {
int t = q[k]; q[k] = q[u]; q[u] = t; // 交换
down(k);
}
}
private static void sort() {
// 筛选法建堆,时间复杂度O(n),大根堆
for (int i = n / 2; i >= 1; i--) down(i);
int size = n;
while (n != 0) {
int t = q[n]; q[n] = q[1]; q[1] = t; // 交换
n--;
down(1);
}
n = size;
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
String[] t = br.readLine().split(" ");
for (int i = 1; i <= n; i++) q[i] = Integer.parseInt(t[i - 1]);
sort();
for (int i = 1; i <= n; i++) System.out.print(q[i] + " ");
System.out.println();
}
}
三. 交换排序
3.1 冒泡排序
分析
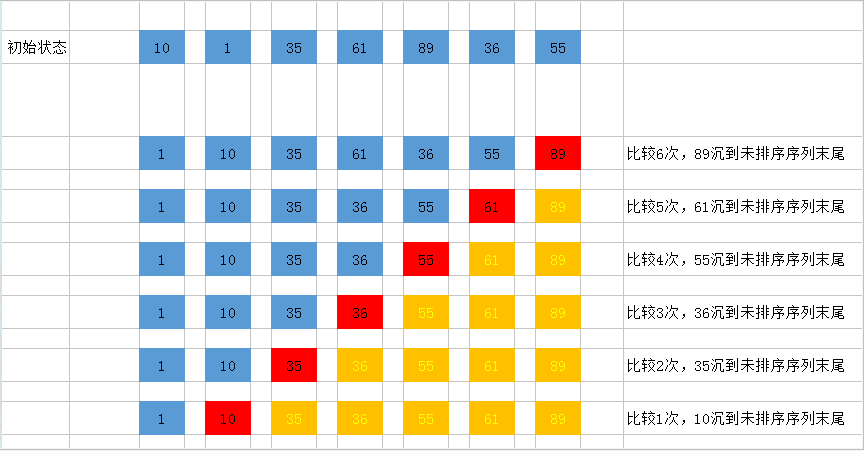
代码
- C++
// Created by WXX on 2021/3/1 15:07
#include <iostream>
using namespace std;
const int N = 1010;
int n;
int q[N];
void sort() {
bool flag = true; // true代表在本轮中交换了某些数据
for (int i = n - 1; i > 0; i--) {
if (!flag) break;
flag = false;
for (int j = 0; j < i; j++)
if (q[j] > q[j + 1]) {
flag = true;
swap(q[j], q[j + 1]);
}
}
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &q[i]);
sort();
for (int i = 0; i < n; i++) printf("%d ", q[i]);
printf("");
return 0;
}
- Java
import java.util.Scanner;
/**
* Created by WXX on 2021/3/1 15:16
*/
public class Main {
public static final int N = 1010; // 输入数据个数的的上限
static int n; // 实际元素个数
static int[] q = new int[N];
private static void sort() {
boolean flag = true; // true代表在本轮中交换了某些数据
for (int i = n - 1; i > 0; i--) {
if (!flag) break;
flag = false;
for (int j = 0; j < i; j++)
if (q[j] > q[j + 1]) {
flag = true;
int t = q[j]; q[j] = q[j + 1]; q[j + 1] = t;
}
}
}
public static void main(String[] args) {
Scanner sn = new Scanner(System.in);
n = sn.nextInt();
for (int i = 0; i < n; i++) q[i] = sn.nextInt();
sort();
for (int i = 0; i < n; i++) System.out.print(q[i] + " ");
System.out.println();
}
}
3.2 快速排序
分析
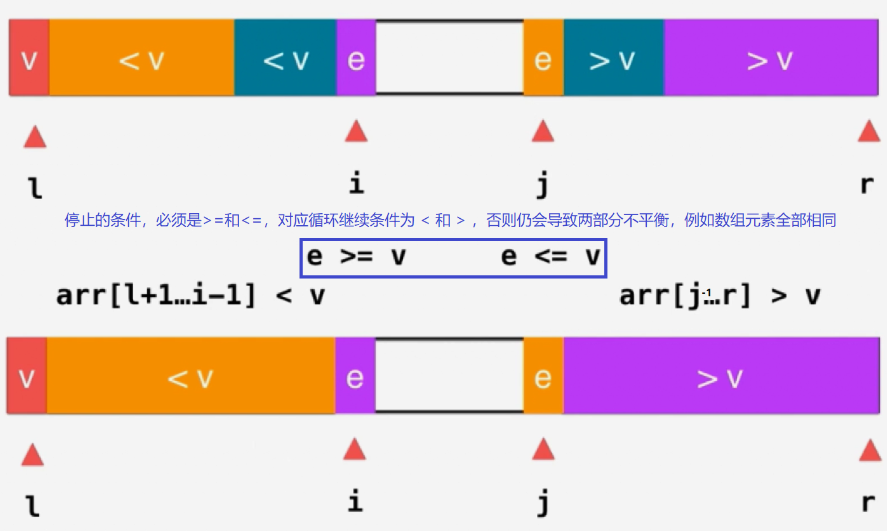
代码
- C++
// Created by WXX on 2021/3/1 15:51
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int q[N];
void quick_sort(int l, int r) {
if (l >= r) return;
int x = q[(l + r) / 2], i = l - 1, j = r + 1;
while(i < j) {
while(q[++i] < x);
while(q[--j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(l, j);
quick_sort(j + 1, r);
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &q[i]);
quick_sort(0, n - 1);
for (int i = 0; i < n; i++) printf("%d ", q[i]);
return 0;
}
- Java
import java.io.BufferedReader;
import java.io.InputStreamReader;
/**
* Created by WXX on 2021/3/1 16:06
*/
public class Main {
public static final int N = 100010;
static int n;
static int[] q = new int[N];
private static void sort(int l, int r) {
if (l >= r) return;
int x = q[(l + r) / 2], i = l - 1, j = r + 1;
while (i < j) {
while (q[++i] < x) ;
while (q[--j] > x) ;
if (i < j) {
int t = q[i]; q[i] = q[j]; q[j] = t;
}
}
sort(l, j);
sort(j + 1, r);
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
String[] t = br.readLine().split(" ");
for (int i = 0; i < n; i++) q[i] = Integer.parseInt(t[i]);
sort(0, n - 1);
for (int i = 0; i < n; i++) System.out.print(q[i] + " ");
System.out.println();
}
}
四. 归并排序
4.1 二路归并排序
分析
- 自顶向下归并排序
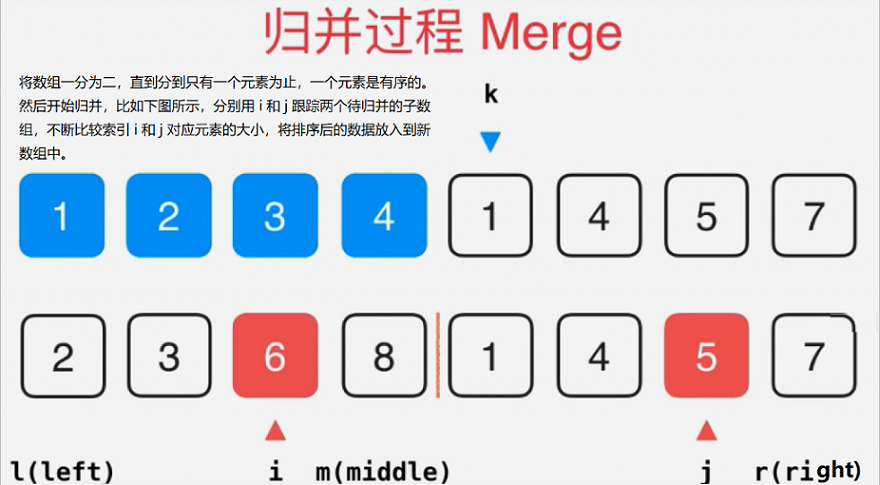
- 自底向上进行归并
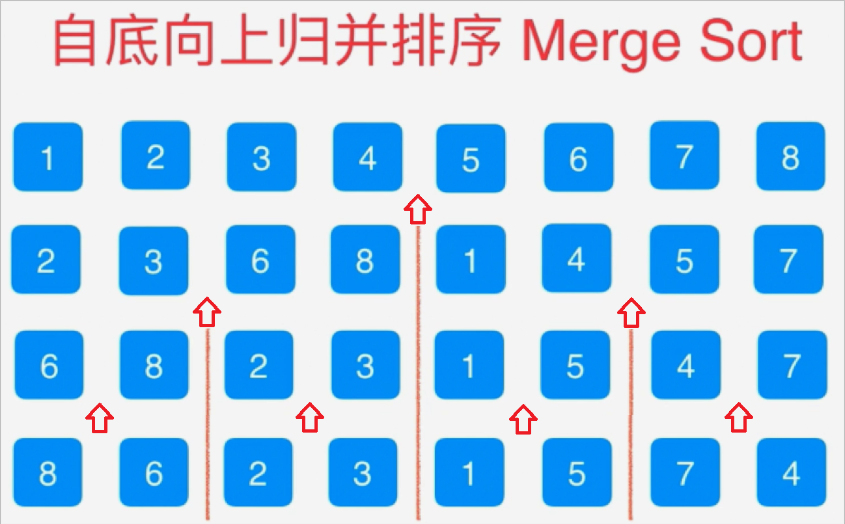
代码
- C++
// Created by WXX on 2021/3/1 16:27
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int q[N], tmp[N];
// 自顶向下归并排序
void merge_sort(int l, int r) {
if (l >= r) return;
int mid = l + r >> 1;
merge_sort(l, mid), merge_sort(mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
while (i <= mid) tmp[k++] = q[i++];
while (j <= r) tmp[k++] = q[j++];
for(i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &q[i]);
merge_sort(0, n - 1);
for (int i = 0; i < n; i++) printf("%d ", q[i]);
return 0;
}
// Created by WXX on 2021/3/1 16:57
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int q[N], tmp[N];
// 自底向上归并排序
void merge_sort() {
for (int sz = 1; sz < n; sz += sz) // 每次合并的两个数组的长度
for (int l = 0; l + sz < n; l += sz + sz) {
int mid = l + sz - 1, r = min(l + sz + sz - 1, n - 1);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
while (i <= mid) tmp[k++] = q[i++];
while (j <= r) tmp[k++] = q[j++];
for (i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
}
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &q[i]);
merge_sort();
for (int i = 0; i < n; i++) printf("%d ", q[i]);
return 0;
}
- Java
import java.io.BufferedReader;
import java.io.InputStreamReader;
/**
* Created by WXX on 2021/3/1 16:30
*/
public class Main {
public static final int N = 100010;
static int n;
static int[] q = new int[N], tmp = new int[N];
// 自顶向下归并排序
private static void sort(int l, int r) {
if (l >= r) return;
int mid = l + r >> 1;
sort(l, mid); sort(mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
while (i <= mid) tmp[k++] = q[i++];
while (j <= r) tmp[k++] = q[j++];
for (i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
String[] t = br.readLine().split(" ");
for (int i = 0; i < n; i++) q[i] = Integer.parseInt(t[i]);
sort(0, n - 1);
for (int i = 0; i < n; i++) System.out.print(q[i] + " ");
System.out.println();
}
}
import java.io.BufferedReader;
import java.io.InputStreamReader;
/**
* Created by WXX on 2021/3/1 16:30
*/
public class Main {
public static final int N = 100010;
static int n;
static int[] q = new int[N], tmp = new int[N];
// 自底向上归并排序
private static void sort() {
for (int sz = 1; sz < n; sz += sz) // 每次合并的两个数组的长度
for (int l = 0; l + sz < n; l += sz + sz) {
int mid = l + sz - 1, r = Math.min(l + sz + sz - 1, n - 1);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
while (i <= mid) tmp[k++] = q[i++];
while (j <= r) tmp[k++] = q[j++];
for (i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
}
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
String[] t = br.readLine().split(" ");
for (int i = 0; i < n; i++) q[i] = Integer.parseInt(t[i]);
sort();
for (int i = 0; i < n; i++) System.out.print(q[i] + " ");
System.out.println();
}
}
Leetcode中自底向上归并排序的应用
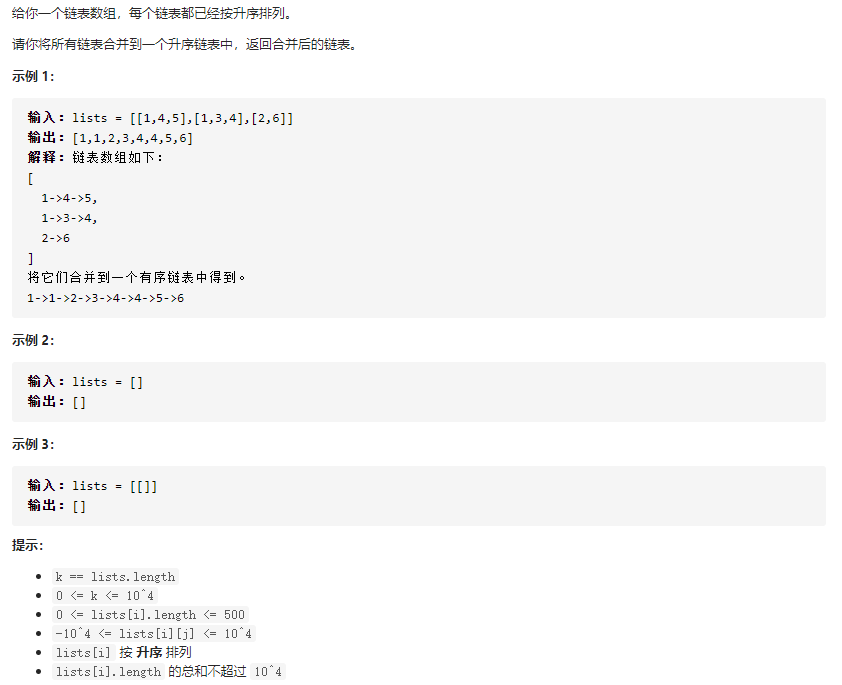
- 代码
C++
/**
* 执行用时:24 ms, 在所有 C++ 提交中击败了93.76%的用户
* 内存消耗:13.1 MB, 在所有 C++ 提交中击败了70.38%的用户
*/
class Solution {
public:
ListNode *merge(ListNode *l1, ListNode *l2) {
if (l1 == NULL) return l2;
if (l2 == NULL) return l1;
if (l1->val < l2->val) {
l1->next = merge(l1->next, l2);
return l1;
} else {
l2->next = merge(l1, l2->next);
return l2;
}
}
ListNode *mergeKLists(vector<ListNode *> &lists) {
if (lists.empty()) return NULL;
for (int step = 1; step < lists.size(); step += step)
for (int i = 0; i + step < lists.size(); i += step + step)
lists[i] = merge(lists[i], lists[i + step]);
return lists[0];
}
};
Java
/**
* 执行用时:3 ms, 在所有 Java 提交中击败了76.22%的用户
* 内存消耗:40.7 MB, 在所有 Java 提交中击败了12.53%的用户
*/
public class Solution {
// 返回l1和l2合并后链表的头结点
private ListNode mergeTwoList(ListNode l1, ListNode l2) {
if (l1 == null || l2 == null)
return l1 == null ? l2 : l1;
else if (l1.val < l2.val) {
l1.next = mergeTwoList(l1.next, l2);
return l1;
} else {
l2.next = mergeTwoList(l1, l2.next);
return l2;
}
}
public ListNode mergeKLists(ListNode[] lists) {
if (lists == null || lists.length == 0) return null;
for (int step = 1; step < lists.length; step += step) // 每次合并的两个链表的索引差值
for (int i = 0; i + step < lists.length; i += (step + step)) // i 代表两个待合并链表中的第一个
lists[i] = mergeTwoList(lists[i], lists[i + step]); // list[i] 和 list[i+step] 进行合并
return lists[0];
}
}
- 当然这个题目还有其他解法,比如优先队列实现,这里就不展示代码了
五. 非比较排序
5.1 计数排序
问题描述
- 如果存在一组数据,这些数据的值都位于0~k之间,请给这组数据排序。
分析
- 因为数据都在0~k之间,因此我们可以新开一个数组c,记录各个数据出现的次数。
- 之后对数组c求前缀和,结果仍然存入c中,则此时c[k]代表的含义是小于等于 k 的数据的个数为c[k]个,因此最终 数据i 应该被存放在 索引c[i]-1 处。
- 按照上述描述将结果存入到另一个数组中即可。
- 参考网址
代码
- C++
// Created by WXX on 2021/3/1 20:02
#include <iostream>
#include <cstring>
using namespace std;
const int N = 100010;
int n, k; // 数据个数n,数据范围0~k
int q[N];
void sort() {
// 将数组q拷贝一份到tmp中,目的是让最终排序结果存储在q中
int tmp[N];
memcpy(tmp, q, n * sizeof(int));
// 统计各数据出现次数,然后计算每个数据应该存放的下标
int c[k + 1];
for (int i = 0; i < n; i++) c[tmp[i]]++;
for (int i = 1; i <= k; i++) c[i] += c[i - 1];
// 将数据放到应该存放的位置
for (int i = 0; i < n; i++) q[--c[tmp[i]]] = tmp[i];
}
int main() {
/*
* 测试数据
* 12 4
* 0 3 2 2 2 1 3 0 1 2 0 0
*/
scanf("%d%d", &n, &k);
for (int i = 0; i < n; i++) scanf("%d", &q[i]);
sort();
for (int i = 0; i < n; i++) printf("%d ", q[i]);
return 0;
}
- Java
import java.io.BufferedReader;
import java.io.InputStreamReader;
/**
* Created by WXX on 2021/3/1 20:17
*/
public class Main {
public static final int N = 100010;
static int n, k; // 数据个数n,数据范围0~k
static int[] q = new int[N];
private static void sort() {
// 将数组q拷贝一份到tmp中,目的是让最终排序结果存储在q中
int[] tmp = new int[N];
System.arraycopy(q, 0, tmp, 0, n);
// 统计各数据出现次数,然后计算每个数据应该存放的下标
int[] c = new int[k + 1];
for (int i = 0; i < n; i++) c[tmp[i]]++;
for (int i = 1; i <= k; i++) c[i] += c[i - 1];
// 将数据放到应该存放的位置
for (int i = 0; i < n; i++) q[--c[tmp[i]]] = tmp[i];
}
public static void main(String[] args) throws Exception {
/*
* 测试数据
* 12 4
* 0 3 2 2 2 1 3 0 1 2 0 0
*/
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] t = br.readLine().split(" ");
n = Integer.parseInt(t[0]); k = Integer.parseInt(t[1]);
t = br.readLine().split(" ");
for (int i = 0; i < n; i++) q[i] = Integer.parseInt(t[i]);
sort();
for (int i = 0; i < n; i++) System.out.print(q[i] + " ");
System.out.println();
}
}
5.2 桶排序
问题描述
- 给你一组数据分布范围较大,但数据个数相对较少的数据,对这组数据进行排序。
分析
- 桶排序步骤:
(1)确定桶的个数M,将待排序集合中处于同一个值域的元素存入同一个桶中;
(2)桶内使用各种现有的算法进行排序;
(3)从小到大依次收集每一个桶,最终得到结果。
-
桶排序和快排的关系:快排相当于用两个桶收集数据,但快排没有开辟额外空间。
-
桶排序和计数排序的关系:计数排序是桶排序的一种特殊情况,当桶的大小和数据范围相同时,每个桶中只会存放一个数据的个数,此时桶排序演化成了计数排序。桶排序可以看成是对时间和空间开销的一种折中方案。
代码
- C++
// Created by WXX on 2021/3/1 20:50
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int q[N];
// 读取数据的过程中记录最大值、最小值。初始设为负无穷、正无穷
int maxv = -2e9, minv = 2e9;
void bucket_sort() {
const int K = 10; // 每个桶中数据的个数,可以认为数超参数
int M = (maxv - minv) / K + 1; // 桶的个数
vector<vector<int>> bucket(M); // M个桶
// 收集
for (int i = 0; i < n; i++) bucket[(q[i] - minv) / K].push_back(q[i]);
// 对每个桶中的数据进行排序
for (int i = 0; i < M; i++) sort(bucket[i].begin(), bucket[i].end());
// 收集
for (int i = 0, j = 0, k = 0; i < n;) { // 当前收集到第j个桶的第k个数据
if (k < bucket[j].size()) q[i++] = bucket[j][k++];
else j++, k = 0;
}
}
int main() {
/*
* 测试数据
* 20
* -7 51 3 121 -3 32 21 43 4 25 56 77 16 22 87 56 -10 68 99 70
*/
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &q[i]);
maxv = max(maxv, q[i]);
minv = min(minv, q[i]);
}
bucket_sort();
for (int i = 0; i < n; i++) printf("%d ", q[i]);
return 0;
}
- Java
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
/**
* Created by WXX on 2021/3/1 21:18
*/
public class Main {
public static final int N = 100010;
static int n;
static int[] q = new int[N];
// 读取数据的过程中记录最大值、最小值。初始设为负无穷、正无穷
static int maxv = Integer.MIN_VALUE, minv = Integer.MAX_VALUE;
private static void bucketSort() {
final int K = 10; // 每个桶中数据的个数,可以认为数超参数
int M = (maxv - minv) / K + 1; // 桶的个数
List<List<Integer>> bucket = new ArrayList<>(M); // M个桶
for (int i = 0; i < M; i++) bucket.add(new ArrayList<>());
// 收集
for (int i = 0; i < n; i++) bucket.get((q[i] - minv) / K).add(q[i]);
// 对每个桶中的数据进行排序
for (int i = 0; i < M; i++) Collections.sort(bucket.get(i));
// 收集
for (int i = 0, j = 0, k = 0; i < n; ) { // 当前收集到第j个桶的第k个数据
if (k < bucket.get(j).size()) q[i++] = bucket.get(j).get(k++);
else {
j++; k = 0;
}
}
}
public static void main(String[] args) throws Exception {
/*
* 测试数据
* 20
* -7 51 3 121 -3 32 21 43 4 25 56 77 16 22 87 56 -10 68 99 70
*/
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
String[] t = br.readLine().split(" ");
for (int i = 0; i < n; i++) {
q[i] = Integer.parseInt(t[i]);
maxv = Math.max(maxv, q[i]);
minv = Math.min(minv, q[i]);
}
bucketSort();
for (int i = 0; i < n; i++) System.out.print(q[i] + " ");
System.out.println();
}
}
5.3 基数排序
问题描述
- 给你一组非负整数(0~INT_MAX),请对这些数据进行排序。
分析
-
基数排序也可以称为多关键字排序,也是一种非比较性质的排序算法。
-
基数排序在桶排序的基础上做了优化,桶排序需要选择适当的映射规则,来完成集合中元素到多个桶的映射,也可以称之为值域划分。但是当集合中元素跨度很大时,映射规则的设计比较困难,若规则设计的宽泛一些,则桶的个数较少,随便避免了许多空桶的情况,但是可能会存在元素分布不均,桶排序则演变为普通的比较性质排序;若规则设计的较为精确,则桶的个数较多,可能会存在大部分桶都是空桶的情况,存在较大空间浪费。
-
桶排序之所以存在上述问题,原因在于算法中对待排序元素的属性选择所致。排序过程选择使用了元素本身的 “大小” 属性,所以算法处理的元素集合就是这个 “大小” 空间。例如,若待排序元素为整型,而整型数字在 “大小” 方面可以是无限大或者无限小的;若待排序元素为字符串,而字符串在 “长度” 方面是无限大的。而桶排序又是一种对元素总容量敏感的排序算法,所以存在使用限制。
-
算法过程(采用LSD,即最低位优先法)
(1)根据待排序元素的类型申请桶空间,并从待排序集合中计算出元素的最大位数;
(2)从右向左,根据元素当前位数的值,将所有元素移动到对应的桶中;
(3)将所有桶中元素移动回原始集合中;
(4)重复步骤 2, 3,直到遍历完所有位数。
-
关于 最高位优先MSD法 和 最低位优先LSD法
n 个记录的序列 {$R_1,R_2,…,R_n$},对关键字 ($K_i^{d-1},K_i^{d-2},…,K_i^0$) 有序是指(d表示数据的最多位数):对于序列中任意两个记录 $R_i$ 和 $R_j$ (1≤i<j≤n) 都满足下列(词典)有序关系: ($K_i^{d-1},K_i^{d-2},…,K_i^0$) < ($K_j^{d-1},K_j^{d-2},…,K_j^0$) ,则 $K^{d-1}$ 被称为 最主关键字,$K^0$ 被称为 最次关键字。
最高位优先LSD法:先对 $K^{d-1}$ 进行桶排序排序,再对 $K^{d-2}$ 进行桶排序,……, 依次类推,直至最后对最低位关键字桶排序完成为止。
最低位优先MSD法:先对 $K^0$ 进行桶排序排序,再对 $K^1$ 进行桶排序,……, 依次类推,直至最后对最高位关键字桶排序完成为止。
代码
- C++
// Created by WXX on 2021/3/1 22:25
#include <iostream>
#include <cmath>
#include <vector>
using namespace std;
const int N = 100010, RADIX = 10; // 十进制数据
int n;
int q[N];
int d; // 输入的最大数据的位数
int base[10]; // base[i] = 10 ^ i
void sort() {
vector<vector<int>> f(RADIX); // 负责收集数据的数组
for (int i = 0; i < d; i++) {
// 分配
for (int j = 0; j < n; j++) f[(q[j] / base[i]) % RADIX].push_back(q[j]);
// 收集
for (int ii = 0, j = 0, k = 0; ii < n;) { // 当前收集到第j个桶的第k个数据
if (k < f[j].size()) q[ii++] = f[j][k++];
else j++, k = 0;
}
for (auto &v : f) v.clear(); // &不能省略
}
}
int main() {
/*
* 测试数据
* 10
* 1086 187 30 76 0 1359 36 777 9 2
*/
// 输入要求:必须大于等于0
int maxv = -2e9; // 用于计算数据的位数
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &q[i]);
maxv = max(maxv, q[i]);
}
d = ceil(log10(maxv + 1));
base[0] = 1;
for (int i = 1; i < 10; i++) base[i] = base[i - 1] * 10;
sort();
for (int i = 0; i < n; i++) printf("%d ", q[i]);
return 0;
}
- Java
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
/**
* Created by WXX on 2021/3/1 22:54
*/
public class Main {
public static final int N = 100010, RADIX = 10; // 十进制数据
static int n;
static int[] q = new int[N];
static int d; // 输入的最大数据的位数
static int[] base = new int[10]; // base[i] = 10 ^ i
private static void sort() {
List<List<Integer>> f = new ArrayList<>();
for (int i = 0; i < RADIX; i++) f.add(new ArrayList<>());
for (int i = 0; i < d; i++) {
// 分配
for (int j = 0; j < n; j++) f.get((q[j] / base[i]) % RADIX).add(q[j]);
// 收集
for (int ii = 0, j = 0, k = 0; ii < n; ) { // 当前收集到第j个桶的第k个数据
if (k < f.get(j).size()) q[ii++] = f.get(j).get(k++);
else {
j++; k = 0;
}
}
for (List<Integer> v : f) v.clear();
}
}
public static void main(String[] args) throws Exception {
/*
* 测试数据
* 10
* 1086 187 30 76 0 1359 36 777 9 2
*/
// 输入要求:数组q中的数据必须大于等于0
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
String[] t = br.readLine().split(" ");
int maxv = Integer.MIN_VALUE; // 用于计算数据的位数
for (int i = 0; i < n; i++) {
q[i] = Integer.parseInt(t[i]);
maxv = Math.max(maxv, q[i]);
}
d = (int) Math.ceil(Math.log10(maxv + 1));
base[0] = 1;
for (int i = 1; i < 10; i++) base[i] = base[i - 1] * 10;
sort();
for (int i = 0; i < n; i++) System.out.print(q[i] + " ");
System.out.println();
}
}

