SG函数

• Mex运算：设S是一个非负整数集合。定义mex(S)为求出不属于集合S的最小非负整数的运算，即mex(S)=min{x}，x属于自然数，且x不属于S。

• SG函数：在有向图游戏中，对于每个节点x，设从x出发一共有k条有向边，分别到达 $y_1、y_2、…、y_k$，定义SG(x)为x的后继节点 $y_1、y_2、…、y_k$ 的SG函数值构成的集合再进行mex运算的结果，即 $SG(x)=mex\{SG(y_1)、SG(y_2)、…、SG(y_k)\}$。

• 定义SG(终点)=0，则对于一个有向图游戏对应的有向图，从终点开始可以推出每个点的SG值，下面是一个例子：

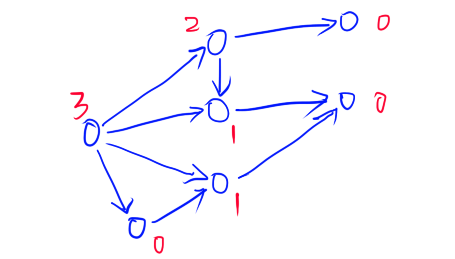
• 如果一个游戏中只存在一个这样的有向图，对于图中的某个点x，如果SG(x)==0，则当前处于x状态的人必败，否则必胜。证明也很容易，如果$SG(x) \neq 0$ 的话，说明其可以让对方到达0状态；如果 $SG(x)==0$，说明必定会让对方到达非0状态，如此往复，先手如果开始为0，则最后一定为0，失败，否则胜利。

• 如果是这样的话，有个问题：SG的值取0和1两种状态是不是就足够了？答案：如果一个游戏中只存在一个有向图这样是可以；但是如果一个游戏存在多个有向图，这样是不可以的。

• 如果存在多个图的话，只有在任意一个图上无法操作了，才是输了。如下图：

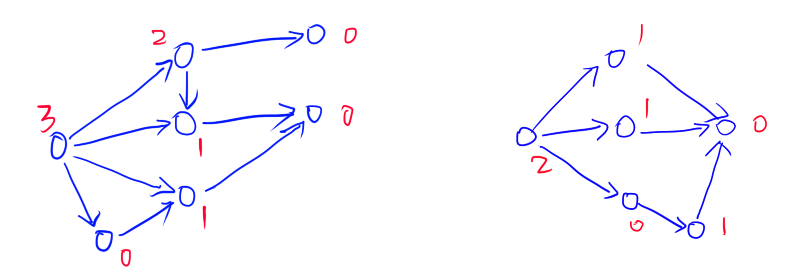
• 那么我们如何判断两个人谁赢呢？结论是我们可以将所有连通分量起点的SG值异或起来，如果不为0，先手必胜，否则先手必败。

• 这是怎么证明的呢？证明方式和上面的Nim游戏一样，只不过经上面的$a_i$换成 $SG(x_i)$ 即可（Nim游戏的每一堆对应这里的每张有向图）。

分析

• 因为有n堆石子，相当于有n个有向图，依次求取每个有向图起点的SG值，将所有这些值异或起来即可，如果不等于0，先手必胜，否则先手必败。

• 假设我们每次只能取2个或者5个石子，只有一堆石子（10个），则对应的有向图以及SG值如下（红色标出的为SG值）：

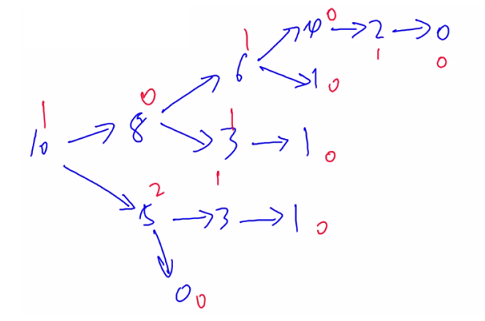
• 那么如何求每个有向图起点的SG值呢？可以使用记忆化搜索。

代码

#include <iostream>
#include <cstring>
#include <unordered_set>

using namespace std;

const int N = 110, M = 10010;

int n, m;  // n: 有多少堆石子, m: 可取的不同数量石子的数量
int s[N];  // 可取石子的数量
int f[M];  // 记忆化搜索, 记录每个节点对应的sg值

int sg(int x) {

    if (f[x] != -1) return f[x];

    unordered_set<int> S;  // 记录从节点x能到达的sg的值
    for (int i = 0; i < m; i++) {
        int t = s[i];
        if (x >= t) S.insert(sg(x - t));
    }

    for (int i = 0; ; i++)
        if (!S.count(i))
            return f[x] = i;
}

int main() {

    cin >> m;
    for (int i = 0; i < m; i++) cin >> s[i];

    cin >> n;

    memset(f, -1, sizeof f);

    int res = 0;
    for (int i = 0; i < n; i++) {
        // 不需要再次初始化f，因为只要输入是一样的，整个图的sg值都唯一
        int x;
        cin >> x;
        res ^= sg(x);
    }

    if (res) puts("Yes");
    else puts("No");

    return 0;
}