题目描述

有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。

第 i 种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

样例

输入样例
4 5
1 2
2 4
3 4
4 5
输出样例：
10
```

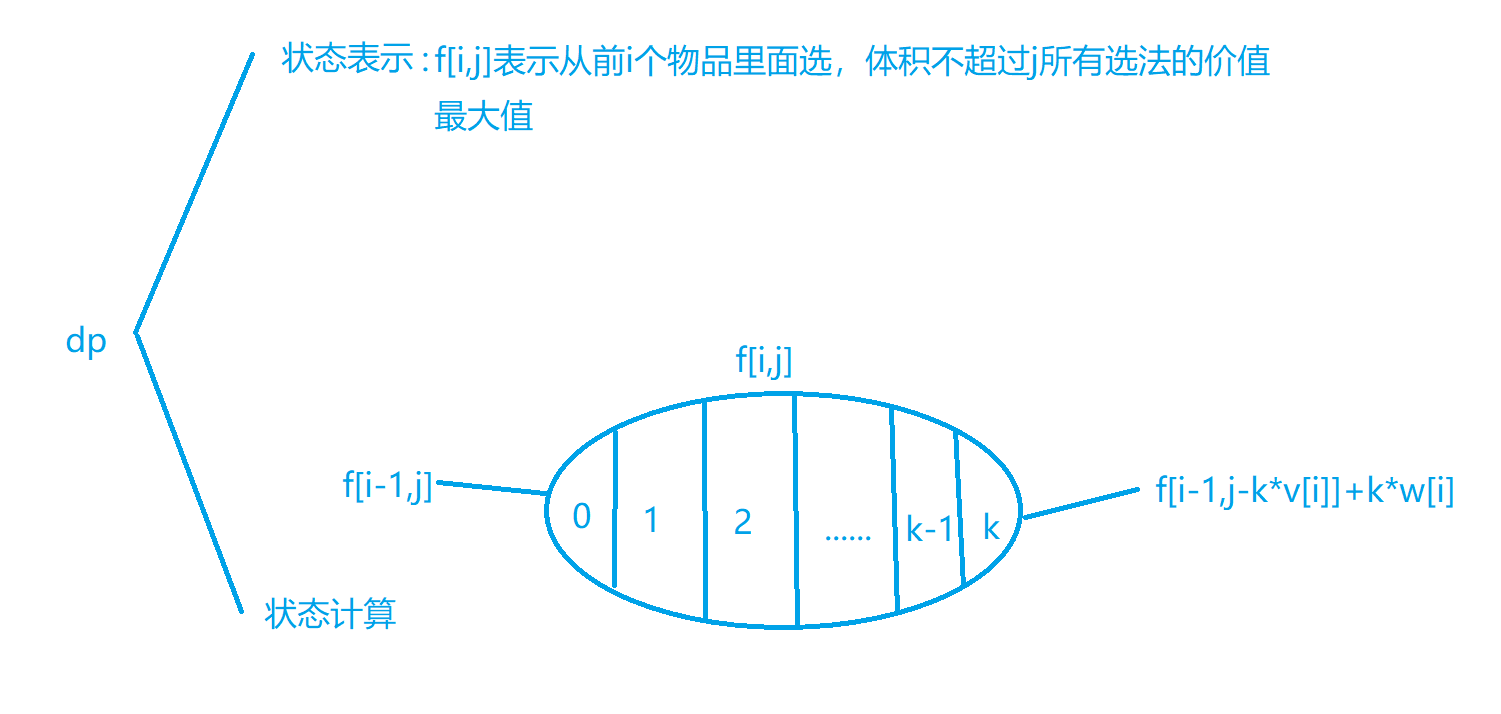时间复杂度$O(n^3)$

状态转移： 选0个到选k个第i个品

#include<iostream>
using namespace std;
const int N=1010;
int v[N],w[N];
int f[N][N];
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)scanf("%d%d",&v[i],&w[i]);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
                for(int k=0;k<=j/v[i];k++)
                    f[i][j]=max(f[i][j], f[i-1][j-k*v[i]]+k*w[i]);
    cout<<f[n][m]<<endl;
    return 0;
}

优化版

时间复杂度$O(n^2)$

状态表达式f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i])

f[i-1][j]表示不选第i个物品，f[i][j-v[i]]表示从前i个物品里面选，但是空出一个空间出来，无论如何，最少选1个第i个物品，最多选k个i个物品

状态的推导 f[i][j]=max(f[i-1][j],f[i-1][j-v]+w,f[i-1][j-2v]+2w,f[i-1][j-3v]+3w....f[i-1][j-kv]+kw)

f[i][j-v]=max(f[i-1][j-v],f[i-1]][j-2v]+w,f[i-1][j-3v]+2w....f[i-1][j-kv]+(k-1)w f[i][j-v]与上面的表达式只相差一个w,计算时候给f[i][j-v]加上w即可

#include<iostream>
using namespace std;
const int N=1010;
int f[N][N];
int w[N],v[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)  
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
        }
    cout<<f[n][m]<<endl;
    return 0;
}

最终优化版

由01背包可知，状态表达式只用到了i和i-1的状态，所以可以将表示i这一维去掉

#include<iostream>
using namespace std;
const int N=1010;
int f[N];//表示选第i个物品空间为j最大值
int w[N],v[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)  
        for(int j=v[i];j<=m;j++)//这里和01背包不一样的地方，是从小到大枚举体积，因为f[j-v[i]]+w[i]原本二维是f[i][j-v[i]+w[i],用到i的状态，而不是01背包里面的i-1的状态
            f[j]=max(f[j],f[j-v[i]]+w[i]);
    cout<<f[m]<<endl;
    return 0;
}