简单记录，看注释即可！

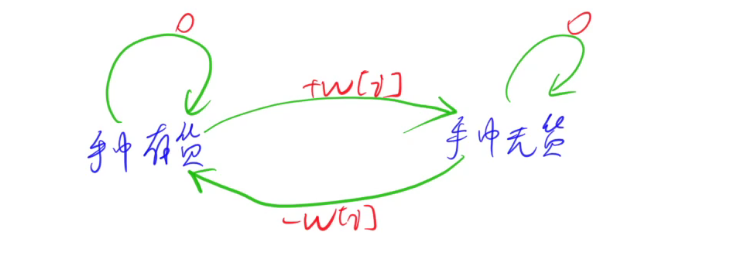
我懒，还是直接附上y总讲解时的的图！

参考代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int n, k, w[N], f[N][110][2];

/*
由于买入->卖出是一次交易：
    1. 若手中有货，则说明当前这次交易正在进行，并没有结束
    2. 若手中无货，则说明当前这次交易已经结束


状态表示：f[i][j][k]：从前i天中选，且经过j次交易，且当前状态为k（0无货，1有货）的集合。的最大值！
    f[i][j][0]：走到第i天，且已经进行了j次交易，且手中无货
    f[i][j][1]：走到第i天，且正在进行第j次交易，且手中有货
状态计算：（从状态机转移图轻松分析得出）
    ->0：f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + w[i]);
    ->1；f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - w[i]);

    关于：f[i - 1][j - 1][0] - w[i] 为 j - 1 解释：
        买入是一次交易。w[i]是第j次交易，未买入前是第j - 1次交易！

    初始化：
        f[i][0][0]：未进行交易也没有或，可能，初始化为0
        f[i][0][1]：未进行交易却有货，不可能，因此为负无穷

    最终答案：在k次交易中选择某次最大交易即可，f[n][i][0]

*/

int main(){
    cin >> n >> k;
    for(int i = 1; i <= n; i ++) cin >> w[i];

    memset(f, -0x3f, sizeof f);
    for(int i = 0; i <= n; i ++) f[i][0][0] = 0;

    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= k; j ++){
            f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + w[i]);
            f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - w[i]);
        }

    // 交易完成一定是无货状态，f[n][i][0]
    int res = 0;
    for(int i = 1; i <= k; i ++) res = max(res, f[n][i][0]);
    cout << res << endl;
    return 0;
}