原理

• 容斥原理属于集合论的内容。

• 如果使用|S|表示集合S中元素的个数，那么高中我们最常见的是三个集合的情形：给定三个集合 $S_1、S_2、S_3$，求这三个集合元素的个数（重复的元素技能计算一次），如下图：

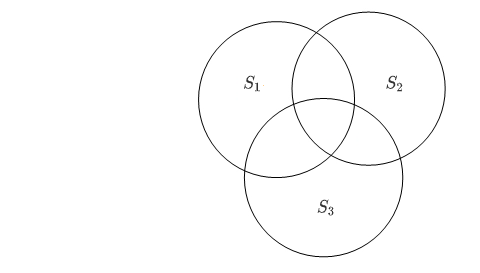
$$ |S_1 \cup S_2 \cup S_3| = |S_1| + |S_2| + |S_3| - |S_1 \cap S_2| - |S_1 \cap S_3|- |S_2 \cap S_3| + |S_1 \cap S_2 \cap S_3| $$

• 推广：对于n个集合，让求解一共出现了多少个元素，则有如下公式：

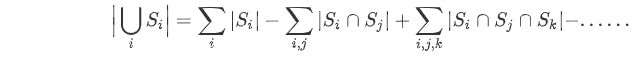
上式就是容斥原理内容。

• 如下是对容斥原理的证明：思路是查看每个元素是否是只被计算了一次，如果是的话，说明公式是正确的。

不妨设元素x在k个集合（$1 \le k \le n$）中出现过，根据公式则其被计算的次数为：
$$ C_k^1 - C_k^2 + C_k^3 - … + (-1)^{k-1}C_k^k $$
根据二项式定理，可知：
$$ C_k^1 - C_k^2 + C_k^3 - … + (-1)^{k-1}C_k^k = -(1 - 1) ^ k + C_k^0 = 1 $$
因此每个元素只计算了一次，该公式是正确的。

• 另外我们考虑一个容斥原理中等式右侧有多少项相加减，第一项相当于从n个元素中拿1个，第二项相当于从n个元素中拿2个，......，因此相加减的项数有：
  $$ C_n^1 + C_n^2 + C_n^3 - … + C_n^n $$
  那么这个式子等于多少呢？如果上面再加上一项$C_n^0$，表示从n个元素中拿0个，则相当于问n个元素有多少个子集，考虑每个元素都可选可不选，因此一共有$2^n$个子集，因此有：
  $$ C_n^0 + C_n^1 + C_n^2 + C_n^3 - … + C_n^n = 2^n $$
  整理可以得到：
  $$ C_n^1 + C_n^2 + C_n^3 - … + C_n^n = 2^n - 1 $$
  一共有$2^n-1$项相加减。

分析

• 最简单的思路是对于每个整数x，判断这m个质数中是否存在能整数x，如果存在，答案加一，这样做法的时间复杂度是$O(n \times m)$的，会TLE，不可取。

• 另一种思路是使用容斥原理，考察能被 $p_i(1 \le i \le m)$，能被 $p_i$ 整除的数的数量为 $\lfloor \frac{n}{p_i} \rfloor$，结果加上这些数量，但是会有重复，比如同时能被两个质数 $p_i, p_j(1 \le i, j \le m)$ 整除的数据被计算了两次，需要减去，......，因此最终的答案：

$$ \sum _ i \lfloor \frac{n}{p_i} \rfloor - \sum _ {i, j} \lfloor \frac{n}{p_i \times p_j} \rfloor + \sum _ {i, j, k} \lfloor \frac{n}{p_i \times p_j \times p_k} \rfloor -...... $$

• 时间复杂度：一共有$2^m-1$项相加减，每次计算主要是质数相乘，最多相乘m-1次，因此时间复杂度为$O(2^m \times m)$。

• 另外还要考虑如何遍历所有的可能组合，这有一个常用的技巧，我们可以通过二进制的方式进行遍历，即从1循环到$2^m-1$，对于其中的每个数据，对应一种集合，该数据的二进制表示中如果某一位是1，代表需要乘上该质数。

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 20;

int p[N];  // 输入的质数

int main() {

    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; i++) cin >> p[i];

    int res = 0;
    for (int i = 1; i < 1 << m; i++) {

        int t = 1, s = 0;  // t表示当前i对应集合中所有质数乘积, s表示集合中数据个数
        for (int j = 0; j < m; j++) 
            if (i >> j & 1) {
                if ((LL)t * p[j] > n) {
                    t = -1;  // 乘积大于n，res不用变
                    break;
                }
                t *= p[j];
                s++;
            }

        if (t != -1) {
            if (s % 2) res += n / t;
            else res -= n / t;
        }
    }

    cout << res << endl;

    return 0;
}