状态机模型解题

做几点解释：

自我理解：状态机就是将一个对于普通DP问题分析时的一个不太好分析大集合，再次通过状态机将其拆解为一个个小集合！

• 本题可以直接使用DP分析（分析结果会使用上两层即 i - 2），但也可以用状态机模型分析（按步来，即 i - 1）
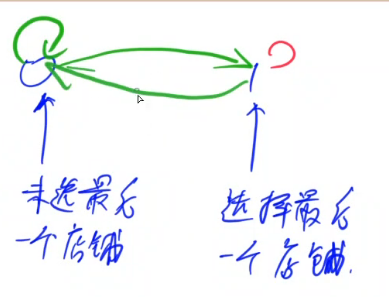
• 图中的箭头其实就是一条可走路径
• 具体来说，箭头起点为前一个点，箭头终点为当前点
• 箭头指向的 1 或 0 代表选与不选

我懒，直接插入y总课中的图片！

参考代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int f[N][2], w[N], T, n;

/*
状态机：
状态表示：
        f[i][j]：表示从前i个里面选择并且第i个物品状态为j的集合的最大值
状态计算：从画出来的状态机模型中分析
        1. ->0的状态：f[i][0] = max(f[i - 1][0], f[i - 1][1])
        2. ->1的状态：f[i][1] = f[i - 1][0] + w[i]

建立虚拟源点0作为状态机的起点！
*/

int main(){
    cin >> T;
    while(T --){
        cin >> n;
        for(int i = 1; i <= n; i ++) cin >> w[i];
        // 这里初始化只要可以保证答案正确即可，都初始化为0也可！但这样初始化似乎会更加清晰！
        f[0][0] = 0, f[0][1] = -1;
        for(int i = 1; i <= n; i ++){
            f[i][0] = max(f[i - 1][0], f[i - 1][1]);
            f[i][1] = f[i - 1][0] + w[i];
        }
        cout << max(f[n][0], f[n][1]) << endl;
    }
    return 0;
}

普通DP

参考代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int f[N], w[N], T, n;

/*
普通DP：
状态表示：
        f[i]：表示从前i个物品中选择的集合中的最大值
状态计算：
        f[i]  选：f[i - 2] + w[i]
        f[i]不选：f[i - 1]
*/

int main(){
    cin >> T;
    while(T --){
        cin >> n;
        for(int i = 1; i <= n; i ++) cin >> w[i];
        f[1] = w[1];
        for(int i = 2; i <= n; i ++) f[i] = max(f[i - 1], f[i - 2] + w[i]);
        cout << f[n] << endl;
    }
    return 0;
}