A 二进制数
小明要用二进制来表示 1 到 10000 的所有整数,要求不同的整数用不同的二进制数表示
请问,为了表示 1 到 10000 的所有整数,至少需要多少个二进制位?
答案
14位
没啥好说的
B 整倍数
请问在 1 到 2020 中,有多少个数既是 4 的整数倍,又是 6 的整数倍。
答案
168
int main(){
int res;
for(int i=1;i<=2020;i++){
if(i%4==0&&i%6==0) res++;
}
cout<<res<<endl;
return 0;
}
C 要求序列
请问有多少个序列满足下面的条件:
1. 序列的长度为 5。
2. 序列中的每个数都是 1 到 10 之间的整数。
3. 序列中后面的数大于等于前面的数。
答案
2002
暴力解,注意看题(是大于等于)
int main(){
int res=0;
for(int a=1;a<=10;a++){
for(int b=a;b<=10;b++){
for(int c=b;c<=10;c++){
for(int d=c;d<=10;d++){
for(int e=d;e<=10;e++){
res++;
}
}
}
}
}
cout<<res<<endl;
return 0;
}
线性DP
推导过程

q[1][1]=q[1][2]=q[1][3]=…=q[1][10]=1
int main(){
int res=0;
int q[10][20];
memset(q,0,sizeof q);
for(int i=1;i<=10;i++){
q[1][i]=1;
}
for(int i=1;i<=5;i++){
for(int j=1;j<=10;j++){
for(int k=1;k<=j;k++){
q[i][j]+=q[i-1][k];
}
}
}
for(int i=1;i<=10;i++){
res+=q[5][i];
}
cout<<res<<endl;
return 0;
}
D 无向图的结点
一个无向图包含 2020 条边,如果图中没有自环和重边,请问最少包含多少个结点?
答案
65
无向完全图,边=(顶点数*(顶点数-1))/2
int main(){
int res=1;
while(1){
if(res*(res-1)>=4040) break;
res++;
}
cout<<res<<endl;
return 0;
}
E 字母距离
两个字母之间的距离定义为它们在字母表中位置的距离。例如 A 和 C 的距离为 2,L 和 Q 的距离为 5。
对于一个字符串,我们称字符串中两两字符之间的距离之和为字符串的内部距离。
例如:ZOO 的内部距离为 22,其中 Z 和 O 的距离为 11。
请问,LANQIAO 的内部距离是多少?
答案
162
仔细读题,关于正负问题。
int main(){
string s="LANQIAO";
int res;
for(int i=0;s[i];i++){
for(int j=i;s[j];j++){
int t=(int)(s[j]-s[i]);
if(t<0) res-=t;
else res+=t;
}
}
cout<<res<<endl;
return 0;
}
F 时间调整
现在时间是 a 点 b 分,请问 t 分钟后,是几点几分?
样例
输入格式
输入的第一行包含一个整数 a。
第二行包含一个整数 b。
第三行包含一个整数 t。
输出格式
输出第一行包含一个整数,表示结果是几点。
第二行包含一个整数,表示结果是几分。
输入
3
20
165
输出
6
5
数据范围
对于所有评测用例,$0 <= a <= 23, 0 <= b <= 59, 0 <= t$, t 分钟后还是在当天。
思路
因为数据都是在当天,所以emmm没啥好说的
C++ 代码
int main(){
int a,b,t;
cin>>a>>b>>t;
b+=t;
a+=b/60;
b%=60;
cout<<a<<endl<<b<<endl;
return 0;
}
G 平行四边形
给定一个平行四边形的底边长度 l 和高度 h,求平行四边形的面积。
样例
输入
2
7
输出
14
思路
emmm有点烦了
C++ 代码
int main(){
int a,b;
cin>>a>>b;
cout<<a*b<<endl;
return 0;
}
H 走方格
小蓝负责花园的灌溉工作。
花园可以看成一个 n 行 m 列的方格图形。中间有一部分位置上安装有出水管。
小蓝可以控制一个按钮同时打开所有的出水管,打开时,有出水管的位置可以被认为已经灌溉好。
每经过一分钟,水就会向四面扩展一个方格,被扩展到的方格可以被认为已经灌溉好。即如果前一分钟某一个方格被灌溉好,则下一分钟它上下左右的四个方格也被灌溉好。
给定花园水管的位置,请问 k 分钟后,有多少个方格被灌溉好?
样例
输入的第一行包含两个整数 n, m。
第二行包含一个整数 t,表示出水管的数量。
接下来 t 行描述出水管的位置,其中第 i 行包含两个数 r, c 表示第 r 行第 c 列有一个排水管。
接下来一行包含一个整数 k。
输入:
3 6
2
2 2
3 4
1
输出
9
样例说明
用1表示灌溉到,0表示未灌溉到。
打开水管时:
000000
010000
000100
1分钟后:
010000
111100
011110
共有9个方格被灌溉好。
数据范围
对于所有评测用例,$1 <= n, m <= 100, 1 <= t <= 10, 1 <= k <= 100$。
思路
BFS就可以了,首先想到的是将每一个灌溉到的都入队,于是自然而然想到用BFS,但是要注意的是,这里需要控制次数,而不能单纯的是队不空,对于队不空其实判断的是何时能将全部土地灌溉结束。而题目中是反过来问的,所以循环里用的是队列初始的长度。
另外需要仔细的是初始处理,就是初始入队以及状态标记和结果初始值不要遗漏掉。
C++ 代码
#include<iostream>
#include<queue>
using namespace std;
const int N=110;
struct Node{
int x,y;
};
queue<Node> q;
bool st[N][N];
int dx[4]={1,-1,0,0};
int dy[4]={0,0,1,-1};
int n,m;
int bfs(){
int a=q.size(); //返回队列中元素的个数
int ans=0;
while(a--){
Node t=q.front();
q.pop();
int x=t.x;
int y=t.y;
for(int i=0;i<4;i++){
int ix=x+dx[i];
int iy=y+dy[i];
if(ix<=0||iy<=0||ix>n||iy>m||st[n][m]) continue;
st[ix][iy]=true;
ans++;
q.push({ix,iy});
}
}
return ans;
}
int main(){
int res=0,t,k;
cin>>n>>m>>t;
res=t;
while(t--){
int r,c;
cin>>r>>c;
q.push({r,c});
st[r][c]=true;
}
cin>>k;
for(int i=0;i<k;i++){
res+=bfs();
}
cout<<res<<endl;
return 0;
}
I
小蓝有一张黑白图像,由 n*m 个像素组成,其中从上到下共 n 行,每行从左到右 m 列。每个像素由一个 0 到 255 之间的灰度值表示。
现在,小蓝准备对图像进行模糊操作,操作的方法为:
对于每个像素,将以它为中心 3 * 3 区域内的所有像素(可能是 9 个像素或少于 9 个像素)求和后除以这个范围内的像素个数(取下整),得到的值就是模糊后的结果。
请注意每个像素都要用原图中的灰度值计算求和。
【输入格式】
输入的第一行包含两个整数 n, m。
第 2 行到第 n + 1 行每行包含 m 个整数,表示每个像素的灰度值,相邻整数之间用一个空格分隔。
【输出格式】
输出 n 行,每行 m 个整数,相邻整数之间用空格分隔,表示模糊后的图像。
样例
输入
3 4
0 0 0 255
0 0 255 0
0 30 255 255
输出
0 42 85 127
5 60 116 170
7 90 132 191
数据范围
对于所有评测用例,$1 <= n, m <= 100$。
思路
首先想到的是用二维前缀和,但是写起来的时候发现并没有省力,于是改用暴力直接算,毕竟数据范围也不是很大。
因为题目是向下取整,所以全程直接用int型进行计算就OKK。
C++ 代码
#include<iostream>
using namespace std;
const int N=110;
int res[N][N],a[N][N];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
int t=a[i-1][j-1]+a[i][j-1]+a[i+1][j-1]+a[i-1][j]+a[i][j]+a[i+1][j]+a[i-1][j+1]+a[i][j+1]+a[i+1][j+1];
if((i==j&&j==1)||(i==n&&j==1)||(i==1&&j==m)||(i==n&&j==m)) t/=4;
else if(i==1||i==n||j==1||j==m) t/=6;
else t/=9;
res[i][j]=t;
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cout<<res[i][j]<<' ';
}
cout<<endl;
}
return 0;
}
J
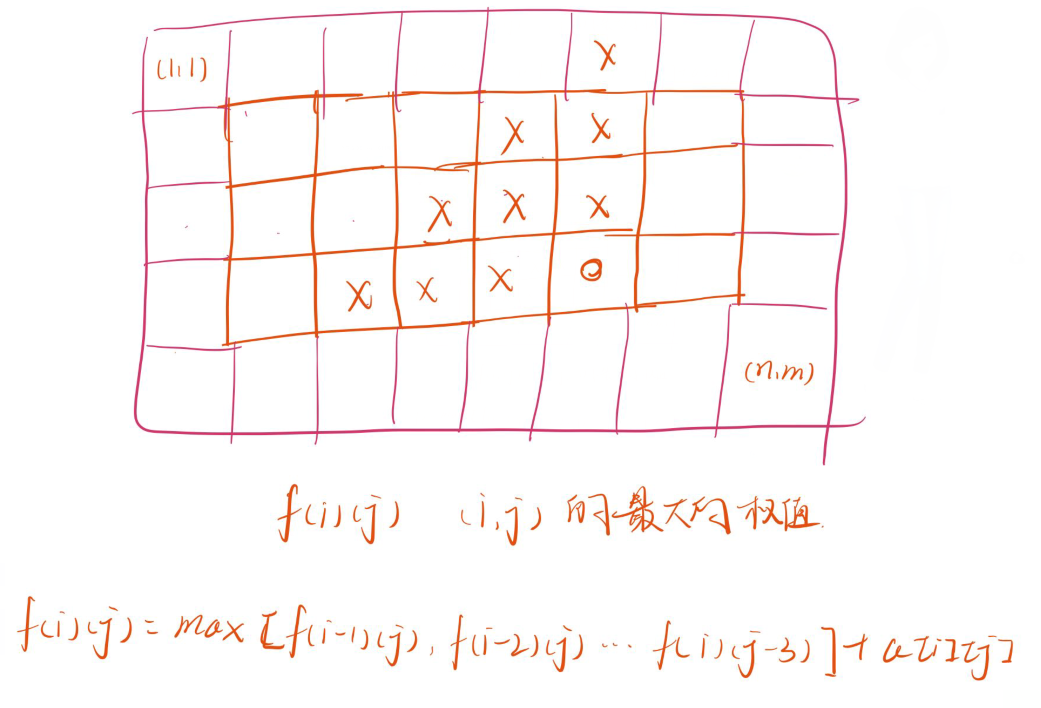
小蓝在一个 n 行 m 列的方格图中玩一个游戏。
开始时,小蓝站在方格图的左上角,即第 1 行第 1 列。
小蓝可以在方格图上走动,走动时,如果当前在第r行第c列,他不能走到行号比r小的行,也不能走到列号比c小的列。同时,他一步走的直线距离不超过3。
例如,如果当前小蓝在第 3 行第 5 列,他下一步可以走到第 3 行第 6 列、第 3 行第 7 列、第 3 行第 8 列、第 4 行第 5 列、第 4 行第 6 列、第 4 行第 7 列、第 5 行第 5 列、第 5 行第 6 列、第 6 行第 5 列之一。
小蓝最终要走到第 n 行第 m 列。
在图中,有的位置有奖励,走上去即可获得,有的位置有惩罚,走上去就要接受惩罚。奖励和惩罚最终抽象成一个权值,奖励为正,惩罚为负。
小蓝希望,从第 1 行第 1 列走到第 n 行第 m 列后,总的权值和最大。请问最大是多少?
输入格式
输入的第一行包含两个整数 n, m,表示图的大小。
接下来 n 行,每行 m 个整数,表示方格图中每个点的权值。
输出格式
输出一个整数,表示最大权值和。
样例
输入
3 5
-4 -5 -10 -3 1
7 5 -9 3 -10
10 -2 6 -10 -4
输出
15
数据范围
对于$30%$的评测用例,$1 <= n, m <= 10$;
对于$50%$的评测用例,$1 <= n, m <= 20$;
对于所有评测用例,$1 <= n, m <= 100,-10000 <= 权值 <= 10000$。
思路
数据范围比较小,所以应该该可以用DFS(不知道后面的数据过不过得了),线性DP也可以做,特别像三角形那一道题
C++ 代码
DFS
#include<iostream>
using namespace std;
const int N=30;
int d[N][N],mp[N][N],res=-0x3f3f3f3f,n,m;
bool s[N][N];
int dx[9]={1,2,3,0,0,0,1,2,1};
int dy[9]={0,0,0,1,2,3,1,1,2};
void dfs(int x,int y){
for(int i=0;i<9;i++){
int ix=x+dx[i];
int iy=y+dy[i];
if(ix>n||iy>m||s[ix][iy]) continue;
d[ix][iy]=d[x][y]+mp[ix][iy];
if(ix==n&&iy==m) res=max(res,d[ix][iy]);
s[ix][iy]=true;
dfs(ix,iy);
s[ix][iy]=false;
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++) cin>>mp[i][j];
}
s[1][1]=true;
d[1][1]=mp[1][1];
dfs(1,1);
cout<<res<<endl;
return 0;
}
线性DP
推导过程,不难,代码中注意对(1,1)点的处理
#include<iostream>
#include<queue>
using namespace std;
const int N=30;
int f[N][N],mp[N][N],n,m;
int dx[9]={-1,-2,-3,0,0,0,-1,-2,-1};
int dy[9]={0,0,0,-1,-2,-3,-1,-1,-2};
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++) cin>>mp[i][j];
}
f[1][1]=mp[1][1];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
int maxv=-0x3f3f3f3f;
if(i==1&&j==1)continue;
for(int k=0;k<9;k++){
if((i+dx[k])<=0||(j+dy[k])<=0) continue;
maxv=max(maxv,f[i+dx[k]][j+dy[k]]);
}
f[i][j]=maxv+mp[i][j];
}
}
cout<<f[n][m]<<endl;
return 0;
}

