核心判断

(i&j)==0&&!hasOdd0[i|j]

这里是当前列的状态是i，而j为上一列的状态。注意到，确保合法有两个条件：

1. 摆放的状态不冲突，即不会出现连续三个的小长条。

2. 两个状态重叠（或）之后，有偶数个零，保证竖着放可行。

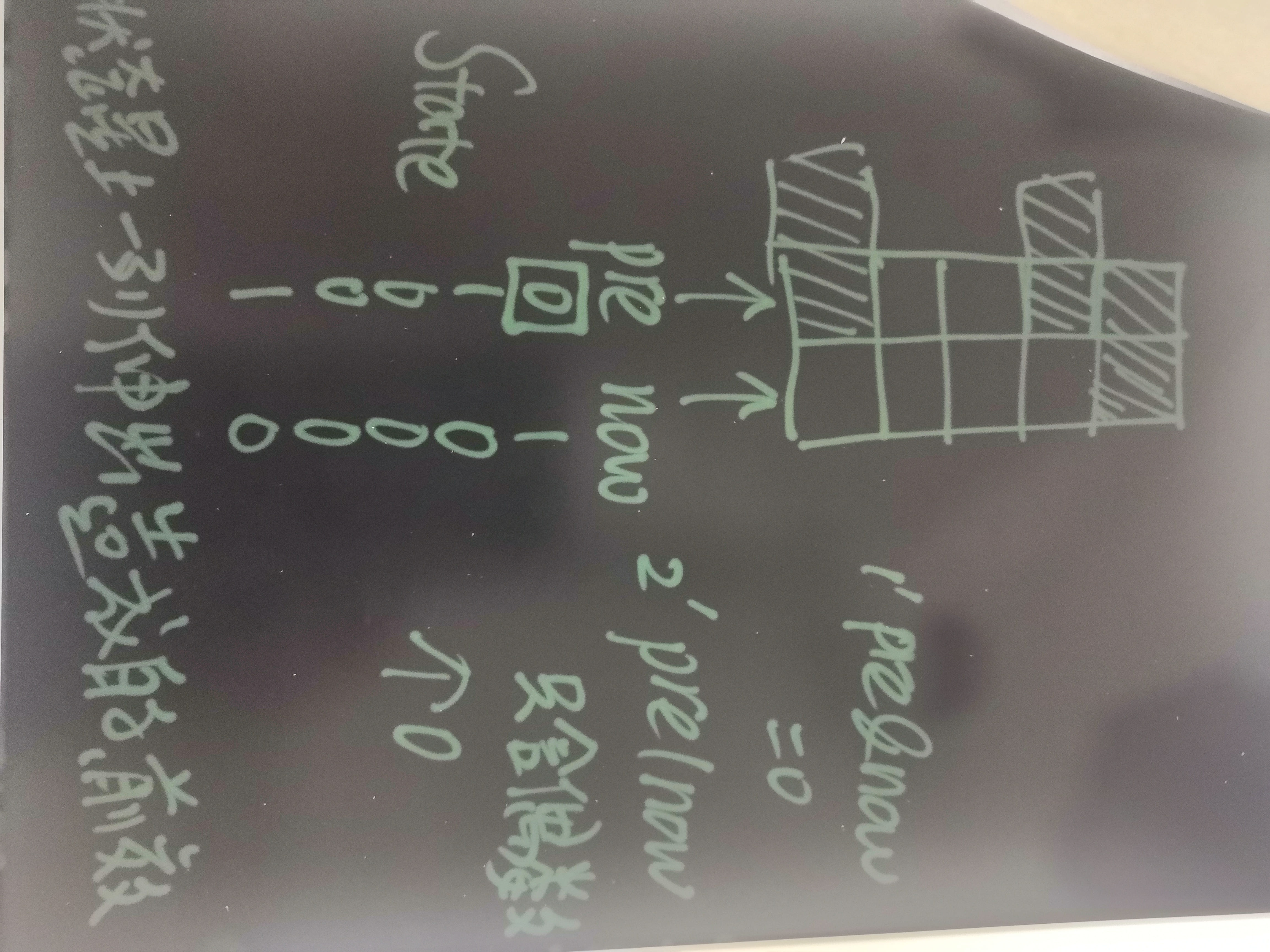
具体逻辑见注释

#include <vector>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;


typedef long long LL;

const int N=12;
const int State=1<<12;

LL f[N][State];//第N列的状态为State时的摆放方案数
vector<int> LegPres[State];//State所有合法的前驱构成它的一个邻接表
bool hasOdd0[State];//记录状态是否含有奇数个零


void initOdd0Arr(int dim);
void initLegPres(int dim);

int main()
{
    int n,m;
    while(cin>>n>>m,m||n){
        initLegPres(n);//一列的状态一共有行数那么多的维度

        memset(f, 0, sizeof f);
        f[0][0]=1;


        //填表f[cols][state]，从列到状态遍历
        for (int i = 1; i <= m; i ++ )
            for (int j = 0; j < (1<<n); j ++ ){
                for(auto preState: LegPres[j]){
                //如果前一列合法，就加上前面的种类数（前面放好了，最后一列是唯一的）
                    f[i][j]+=f[i-1][preState];
                }
            }

        cout<<f[m][0]<<endl;

    }

    return 0;
}

void initOdd0Arr(int dim){
    for(int i=0;i<(1<<dim);i++){

        int cnt=0;
        for(int j=0;j<dim;j++){ 
            if(i>>j &1){
                if(cnt&1) break;//cnt是奇数且下一个不是零
                else cnt=0;//cnt是偶数且下一个不是零
            }else{
                ++cnt;
            }
        }
        hasOdd0[i]=cnt&1;
    }
}
void initLegPres(int dim){
    initOdd0Arr(dim);
    for(int i=0;i<(1<<dim);++i){
        LegPres[i].clear();
        for(int j=0;j<(1<<dim);++j){//对当前状态遍历所有可能的前驱
            if((i&j)==0&&!hasOdd0[i|j])
                LegPres[i].push_back(j);
        }
    }
}