Blog

题目

Luogu
LOJ
Acwing

思路

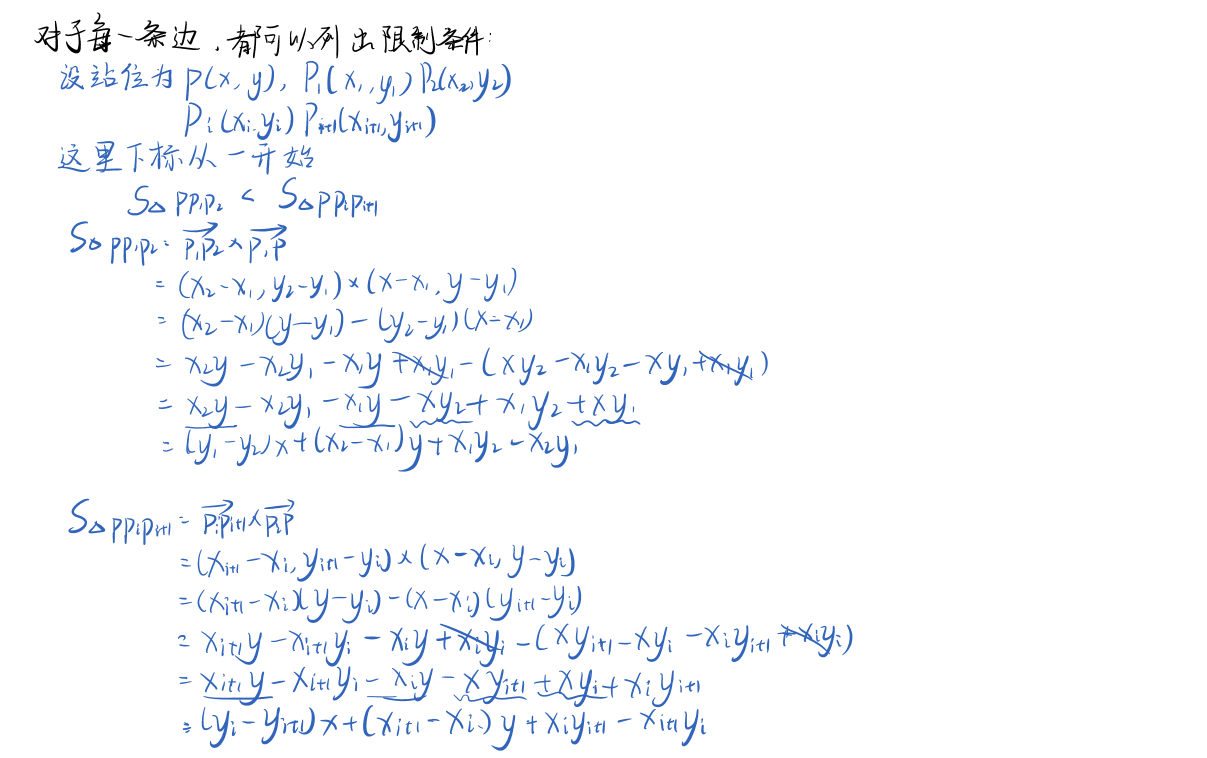
代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdio>
#define x first
#define y second
using namespace std;
typedef pair<double, double> PDD;
const int N = 1000010;
const double eps = 1e-7;
int n, cnt = 0;
PDD P[N], ans[N];
struct LINE { PDD st, ed; } L[N];
inline PDD operator-(PDD a, PDD b) { return make_pair(a.x - b.x, a.y - b.y); }
inline PDD operator+(PDD a, PDD b) { return make_pair(a.x + b.x, a.y + b.y); }
inline PDD operator*(PDD a, double c) { return make_pair(a.x * c, a.y * c); }
inline int cmp(double a, double b) { return (fabs(a - b) < eps) ? 0 : ((a < b) ? -1 : 1); }
inline double cro(PDD a, PDD b) { return a.x * b.y - a.y * b.x; }
inline double area(PDD a, PDD b, PDD c) { return cro(b - a, c - a); }
inline double get_angle(LINE a) { return atan2(a.ed.y - a.st.y, a.ed.x - a.st.x); }
// get_line_intersection 得到直线交点
inline PDD GLI(PDD p, PDD v, PDD q, PDD w) { return p + v * (cro(w, (p - q)) / cro(v, w));}
inline PDD GLI(LINE a, LINE b) { return GLI(a.st, a.ed - a.st, b.st, b.ed - b.st); }
inline bool on_right(LINE a, LINE b, LINE c) {  return cmp(area(a.st, a.ed, GLI(b, c)), 0) < 0; }
inline double get_area(PDD P[], int n) {
    double res = 0;
    for (int i = 2; i + 1 <= n; i++)
        res += cro(P[i] - P[1], P[i + 1] - P[i]);
    return res / 2;
}
inline bool LINE_cmp(LINE a, LINE b) { 
    double A = get_angle(a), B = get_angle(b);
    if (cmp(A, B) == 0) return area(a.st, a.ed, b.ed) < 0;
    else return A < B;
}
int q[N];
inline double HPI() {
    sort(L + 1, L + cnt + 1, LINE_cmp);
    int hh = 0, tt = -1, k = 0;
    for (int i = 1; i <= cnt; i++) {
        if (i != 1 && !cmp(get_angle(L[i]), get_angle(L[i - 1]))) continue;
        while (hh + 1 <= tt && on_right(L[i], L[q[tt - 1]], L[q[tt]])) tt--;
        while (hh + 1 <= tt && on_right(L[i], L[q[hh + 1]], L[q[hh]])) hh++;
        q[++tt] = i;
    }
    while (hh + 1 <= tt && on_right(L[q[hh]], L[q[tt - 1]], L[q[tt]])) tt--;
    while (hh + 1 <= tt && on_right(L[q[tt]], L[q[hh + 1]], L[q[hh]])) hh++;
    q[++tt] = q[hh];
    for (int i = hh; i < tt; i++) ans[++k] = GLI(L[q[i]], L[q[i + 1]]);
    return get_area(ans, k);
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> P[i].x >> P[i].y;
    P[n + 1] = P[1]; // 处理一下, 方便后面
    for (int i = 1; i <= n; i++) L[++cnt] = (LINE) { P[i], P[i + 1] };
    for (int i = 2; i <= n; i++) {
        double A = P[1].y - P[2].y + P[i + 1].y - P[i].y;
        double B = P[2].x - P[1].x + P[i].x - P[i + 1].x;
        double C = -P[2].x * P[1].y + P[1].x * P[2].y + P[i + 1].x * P[i].y - P[i].x * P[i + 1].y;
        if (cmp(B, 0) == 0) L[++cnt] = (LINE) { (PDD){ -C / A, 0 }, (PDD) { -C / A - B, A } };
        else L[++cnt] = (LINE) { (PDD) { 0, -C / B }, (PDD) { -B, -C / B + A }};
    }   
    // 概率就是合法面积除以总面积
    printf("%.4Lf", HPI() / get_area(P, n));
    return 0;
}